题目内容
13、若二次函数f（x）满足f（2+x）=f（2-x）且f（a）≤f（0）＜f（1），则实数a的取值范围是
a≤0或a≥4
．分析：利用满足的恒等式求出二次函数的对称轴；利用对称轴写出二次函数的单调区间；利用f（0）＜f（1），判断出二次函数的单调区间；利用二次函数的单调性求出a的范围．
解答：解：∵二次函数f（x）满足f（2+x）=f（2-x）
∴对称轴为x=2
∴二次函数的单调区间有（-∞，2]；[2，+∞）
∵f（0）＜f（1），
∴f（x）在（-∞，2]递增；在[2，+∞）递减
∵f（0）=f（4），f（a）≤f（0）
∴a≤0或a≥4
故答案为a≤0或a≥4
∴对称轴为x=2
∴二次函数的单调区间有（-∞，2]；[2，+∞）
∵f（0）＜f（1），
∴f（x）在（-∞，2]递增；在[2，+∞）递减
∵f（0）=f（4），f（a）≤f（0）
∴a≤0或a≥4
故答案为a≤0或a≥4
点评：本题考查二次函数的单调性取决于对称轴与二次项的系数、利用二次函数的单调性解不等式．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
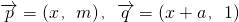，二次函数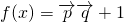
，关于x的不等式f（x）＞（2m-1）x+1-m2的解集为（-∞，m）∪（m+1，+∞），其中m为非零常数，设
．
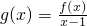时，若x∈[1，3]，求f（x）的最小值；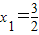
时，探求函数f（x）图象上是否存在点B（x2，y2）（x2＞2），使A、B连线平行于x轴，并说明理由．（参考数据：e=2.71828…）