Question

【题目】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．
如图，在阳马P﹣ABCD中，侧棱PD⊥底面ABCD，且PD=CD，E为PC中点，点F在PB上，且PB⊥平面DEF，连接BD，BE．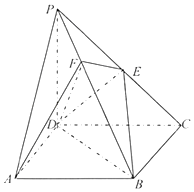

（Ⅰ）证明：DE⊥平面PBC；
（Ⅱ）试判断四面体DBEF是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；
（Ⅲ）已知AD=2， ，求二面角F﹣AD﹣B的余弦值．

Answer 1

【答案】证明：（Ⅰ）因为PD⊥面ABCD，BC面ABCD，

所以BC⊥PD．

因为四边形ABCD为矩形，

所以BC⊥DC．PD∩DC=D，

所以BC⊥面PDC．DE面PDC，DE⊥BC，

在△PDC中，PD=DC，E为PC中点，

所以DE⊥PC．又PC∩BC=C，

所以DE⊥面PBC．

解：（Ⅱ）四面体DBEF是鳖臑，

其中 ， ．

（Ⅲ）以DA，DC，DP所在直线为x轴，y轴，z轴建立空间直角坐标系．

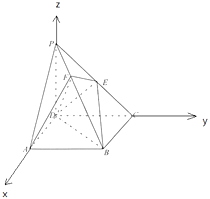
则D（0，0，0），A（2，0，0）， ， ， ．

设 ，则 ．DF⊥PB得 ，解得 ．

所以 ．

设平面FDA的法向量 ，

则 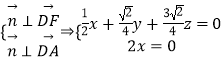，令z=1得x=0，y=﹣3．

平面FDA的法向量 ，

平面BDA的法向量 ，

， ．

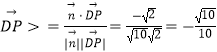二面角F﹣AD﹣B的余弦值为 ．

【解析】（1）推出BC⊥PD，BC⊥DC，从而得出BC⊥面PDC，进而DE⊥BC，再求出DE⊥PC，由此证明DE⊥面PBC；（2）四面体DBEF是鳖臑，写出直角；（3）以D为坐标原点，DA，DC，DP分别为x，y，z轴建立空间直角坐标系，用法向量求出二面角的余弦值.