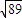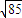题目内容
已知P是椭圆 上的点,Q、R分别是圆
上的点,Q、R分别是圆 上的点,则|PQ|+|PR|的最小值是
上的点,则|PQ|+|PR|的最小值是
- A.

- B.
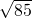
- C.10
- D.9
D
分析:确定圆的圆心坐标,再利用椭圆的定义,即可求|PQ|+|PR|的最小值.
解答:由题可知两圆 的圆心恰为椭圆的两焦点F1(-4,0)和F2(4,0),
的圆心恰为椭圆的两焦点F1(-4,0)和F2(4,0),
由椭圆的定义知|PF1|+|PF2|=2a=10,从而可得|PQ|+|PR|的最小值为 .
.
故选D.
点评:本题考查椭圆的定义,考查圆的方程,正确运用椭圆的定义是关键.
分析:确定圆的圆心坐标,再利用椭圆的定义,即可求|PQ|+|PR|的最小值.
解答:由题可知两圆
 的圆心恰为椭圆的两焦点F1(-4,0)和F2(4,0),
的圆心恰为椭圆的两焦点F1(-4,0)和F2(4,0),由椭圆的定义知|PF1|+|PF2|=2a=10,从而可得|PQ|+|PR|的最小值为
 .
.故选D.
点评:本题考查椭圆的定义,考查圆的方程,正确运用椭圆的定义是关键.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 上的点,F1、F2分别是椭圆的左、右焦点,若
上的点,F1、F2分别是椭圆的左、右焦点,若 ,则
,则 的面积为(
)
的面积为(
) B、2
B、2
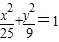 上的点,Q、R分别是圆
上的点,Q、R分别是圆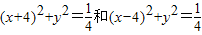 上的点,则|PQ|+|PR|的最小值是( )
上的点,则|PQ|+|PR|的最小值是( )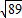
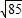
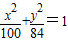 上的点,Q、R分别是圆(x+4)2+y2=1和圆(x-4)2+y2=1 上的点,则|PQ|+|PR|的最小值是( )
上的点,Q、R分别是圆(x+4)2+y2=1和圆(x-4)2+y2=1 上的点,则|PQ|+|PR|的最小值是( )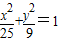 上的点,Q、R分别是圆
上的点,Q、R分别是圆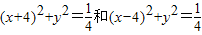 上的点,则|PQ|+|PR|的最小值是( )
上的点,则|PQ|+|PR|的最小值是( )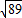
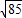
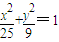 上的点,Q、R分别是圆
上的点,Q、R分别是圆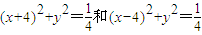 上的点,则|PQ|+|PR|的最小值是( )
上的点,则|PQ|+|PR|的最小值是( )