题目内容
若不等式5+m+
≥k对任意m∈(0,+∞)都成立,则K的最大值为
| 4 | m |
9
9
.分析:令f(m)=5+m+
,m∈(0,+∞),求得f(m)的最小值即可.
| 4 |
| m |
解答:解:∵不等式5+m+
≥k对任意m∈(0,+∞)都成立,
∴k≤f(m)的最小值.
令f(m)=5+m+
,m∈(0,+∞),
则由基本不等式得:f(m)=5+m+
≥5+2
=9(当且仅当m=2时取“=”).
∴f(m)min=9.
∴k≤9.
∴k的最大值为9.
故答案为:9.
| 4 |
| m |
∴k≤f(m)的最小值.
令f(m)=5+m+
| 4 |
| m |
则由基本不等式得:f(m)=5+m+
| 4 |
| m |
m•
|
∴f(m)min=9.
∴k≤9.
∴k的最大值为9.
故答案为:9.
点评:本题考查基本不等式,考查构造函数的思想,考查恒成立问题,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
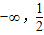 ].求a的值;
].求a的值;