Question

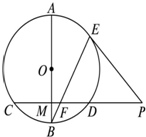
选修4-1：几何证明选讲
如图，已知⊙O中，直径AB垂直于弦CD，垂足为M，P是CD延长线上一点，PE切⊙O于点E，连接BE交CD于点F，证明：
（1）∠BFM=∠PEF；
（2）PF²=PD•PC．

Answer 1

分析：（1）如图所示，连接OE．利用切线的性质可得：OE⊥PE，于是∠PEF+∠OEF=90°．由已知AB⊥CD，可得∠OBF+∠BFM=90°．由同圆的半径相等可得∠OBF=∠OEB．即可得出结论．
（2）利用（1）可得∠PEF=∠PFE．于是PE=PF．利用“切割线定理”可得PE²=PD•PC．即可．

解答：证明：（1）如图所示，连接OE．∵PE切⊙O于点E，∴OE⊥PE，
∴∠PEF+∠OEF=90°．
∵AB⊥CD，∴∠OBF+∠BFM=90°．
∵OE=OB，∴∠OBF=∠OEB．
∴∠BFM=∠PEF；
（2）∵∠BFM=∠PEF，∠BFM=∠PFE，
∴∠PEF=∠PFE．
∴PE=PF．
∵PE切⊙O于点E，∴PE²=PD•PC．
∴PF²=PD•PC．

点评：本题考查了圆的切线的性质、互余角的关系、同圆的半径相等的性质、切割线定理等基础知识与基本技能方法，属于中档题．