题目内容
已知函数y=f(x)是R上的奇函数,当x≤0时,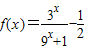 ,
,(1)判断并证明y=f(x)在(-∞,0)上的单调性;
(2)求y=f(x)的值域;
(3)求不等式
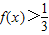 的解集.
的解集.
【答案】分析:(1)利用函数单调性的定义,设x1<x2<0,通过作差,变形,判号证明f(x1)<f(x2),即可
(2)当x≤0时f(x)=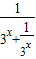 ,运用均值定理,先求出当x≤0时函数f(x)的值域,再利用对称性得y=f(x)的值域
,运用均值定理,先求出当x≤0时函数f(x)的值域,再利用对称性得y=f(x)的值域
(3)由(2)知,不等式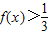 ?
?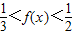 ,将f(x)中的3x看成整体,转化为一元二次方程求解,再解指数不等式即可得所求解集
,将f(x)中的3x看成整体,转化为一元二次方程求解,再解指数不等式即可得所求解集
解答:解:(1)设x1<x2<0,则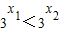 ,
,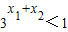
∵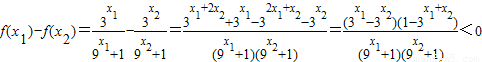 ,
,
∴f(x1)<f(x2),即y=f(x)在(-∞,0)上是增函数.
(2)∵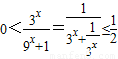 ,
,
∴当x≤0时,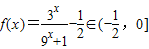 ;
;
∵当x>0时,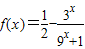
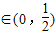 .
.
综上得 y=f(x)的值域为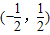 .
.
(3)∵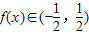 ,
,
又∵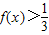 ,∴
,∴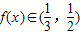 ,此时
,此时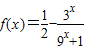 单调递增,
单调递增,
∵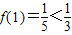 ,∴
,∴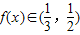 时,x>1⇒3x>3.
时,x>1⇒3x>3.
令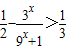 ,
,
即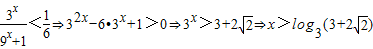 ,
,
∴不等式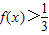 的解集是
的解集是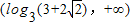 .
.
点评:本题考查了函数奇偶性与单调性的定义及运用,利用函数的单调性和对称性解不等式、求值域的方法,解题时要特别利用对称性,提高解题速度
(2)当x≤0时f(x)=
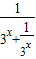 ,运用均值定理,先求出当x≤0时函数f(x)的值域,再利用对称性得y=f(x)的值域
,运用均值定理,先求出当x≤0时函数f(x)的值域,再利用对称性得y=f(x)的值域(3)由(2)知,不等式
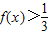 ?
?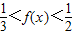 ,将f(x)中的3x看成整体,转化为一元二次方程求解,再解指数不等式即可得所求解集
,将f(x)中的3x看成整体,转化为一元二次方程求解,再解指数不等式即可得所求解集解答:解:(1)设x1<x2<0,则
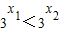 ,
,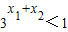
∵
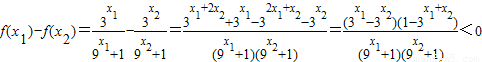 ,
,∴f(x1)<f(x2),即y=f(x)在(-∞,0)上是增函数.
(2)∵
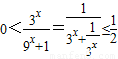 ,
,∴当x≤0时,
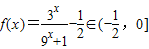 ;
; ∵当x>0时,
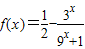
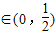 .
. 综上得 y=f(x)的值域为
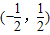 .
. (3)∵
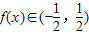 ,
,又∵
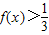 ,∴
,∴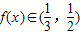 ,此时
,此时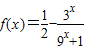 单调递增,
单调递增,∵
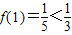 ,∴
,∴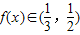 时,x>1⇒3x>3.
时,x>1⇒3x>3.令
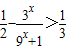 ,
,即
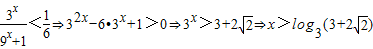 ,
,∴不等式
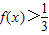 的解集是
的解集是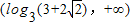 .
.点评:本题考查了函数奇偶性与单调性的定义及运用,利用函数的单调性和对称性解不等式、求值域的方法,解题时要特别利用对称性,提高解题速度

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足