题目内容
如图,正方体ABCD—A1B
NB1,求证:MN⊥MC.
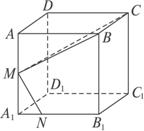
证明:如图,连结BM,
设AB=a,则AM=MA1=,A1N=
,
∴
.
又∠BAM=∠MA1N=90°,
∴△BAM∽△MA1N.
∴∠ABM=∠A1MN.
∵∠ABM+∠AMB=90°,
∴∠AMB+∠A1MN=90°.
∴∠BMN=90°,
即MN⊥MB.
又CB⊥平面ABB
∵MB是MC在平面ABB
∴MN⊥MC.
练习册系列答案
相关题目
题目内容
如图,正方体ABCD—A1BNB1,求证:MN⊥MC.
证明:如图,连结BM,
设AB=a,则AM=MA1=,A1N=,
∴.
又∠BAM=∠MA1N=90°,
∴△BAM∽△MA1N.
∴∠ABM=∠A1MN.
∵∠ABM+∠AMB=90°,
∴∠AMB+∠A1MN=90°.
∴∠BMN=90°,
即MN⊥MB.
又CB⊥平面ABB
∵MB是MC在平面ABB
∴MN⊥MC.
如图正方体ABCD-A1B1C1D1中，M为BC中点，则直线D1M与平面ABCD所成角的正切值为
如图正方体ABCD-A1B1C1D1的棱长为1，点M是棱AA1的中点，点O是BD1的中点，求证：OM是异面直线AA1，BD1的公垂线，并求OM的长．
如图正方体ABCD-A1B1C1D1的棱长为2，则点B1到直线AC的距离是
（文）如图正方体ABCD-A1B1C1D1，在它的12条棱及12条面的对角线所在的直线中，选取若干条直线确定平面，在所有的这些平面中：
甲．如图1，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB：AD=