题目内容
求函数 )的最小值,并求其单调区间.
)的最小值,并求其单调区间.
解:
= .…(4分)
.…(4分)
∵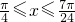 ,∴
,∴ ,∴
,∴ .…(6分)
.…(6分)
当 时,即
时,即  时,函数f(x)取最小值为
时,函数f(x)取最小值为 .…(8分)
.…(8分)
∵ 上递增,…(10分)
上递增,…(10分)
∴ 上是减函数,故函数f(x)的减区间为
上是减函数,故函数f(x)的减区间为 . …(12分)
. …(12分)
分析:利用三角函数的恒等变换化简函数f(x)的解析式为 ,由x的范围可得
,由x的范围可得  ,由此求得函数f(x)取最小值为
,由此求得函数f(x)取最小值为 .再由
.再由 上递增,可得函数f(x)的减区间.
上递增,可得函数f(x)的减区间.
点评:本题主要考查三角函数的恒等变换及化简求值,复合三角函数的单调性和值域,属于中档题.

=
 .…(4分)
.…(4分)∵
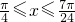 ,∴
,∴ ,∴
,∴ .…(6分)
.…(6分)当
 时,即
时,即  时,函数f(x)取最小值为
时,函数f(x)取最小值为 .…(8分)
.…(8分)∵
 上递增,…(10分)
上递增,…(10分)∴
 上是减函数,故函数f(x)的减区间为
上是减函数,故函数f(x)的减区间为 . …(12分)
. …(12分)分析:利用三角函数的恒等变换化简函数f(x)的解析式为
 ,由x的范围可得
,由x的范围可得  ,由此求得函数f(x)取最小值为
,由此求得函数f(x)取最小值为 .再由
.再由 上递增,可得函数f(x)的减区间.
上递增,可得函数f(x)的减区间.点评:本题主要考查三角函数的恒等变换及化简求值,复合三角函数的单调性和值域,属于中档题.

练习册系列答案
相关题目
 已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,数列{an}的前n项的和Sn=an+1+b、Tn为数列{bn}的前n项的和.且
已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,数列{an}的前n项的和Sn=an+1+b、Tn为数列{bn}的前n项的和.且