题目内容
（本小题满分12分）
设不等边三角形ABC的外心与重心分别为M、G，若A(－1，0)，B(1，0)且MG//AB.
(Ⅰ) 求三角形ABC顶点C的轨迹方程；
(Ⅱ) 设顶点C的轨迹为D，已知直线
过点（0，1）并且与曲线D交于P、N两点，若O为坐标原点，
满足OP⊥ON，求直线的方程.
【解析】：（I）设C（x，y）（xy≠0） …………1分
∵MG∥AB，可设G（a ,b），则M（0，b）.
∴
(1) …………3分
∵M是不等边三解形ABC的外心，∴|MA|=|MC|，
即 
（2） …………4分
由（1）（2）得
.
所以三角形顶点C的轨迹方程为
. …………6分
（II）设直线l的方程为
，
，
，
由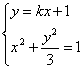
消y得
。 …………8分
∵直线l与曲线D交于P、N两点，∴△=
，
又
，
。
∵
，∴
，∴
…………6分
∴
，∴
。 …………11分
∴直线l的方程为
。 …………12分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
