Question

设a、b是两个实数,集合A={(x,y)|y=ax+b,x∈Z },B={(x,y)|y=3x²+15,x∈Z },C={(x,y)|x²+y²≤144},讨论是否存在实数a和b使得A∩B≠,(a,b)∈C同时成立.

Answer 1

思路分析:把A∩B≠转化为方程组有解的问题.

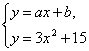解法一:由A∩B≠知方程组有解,

即方程3x²-ax+15-b=0有解.

∴Δ=a²-4×3×(15-b)=a²+12b-180≥0.项基本原则                ①

由(a,b)∈C,得144≥a²+b².                                                   ②

由①②得180-12b≤a²≤144-b².                                            ③

由③得(b-6) ²≤0b=6.

把b=6代入③得108≤a²≤108,

∴a²=108,即a=±6.

把a=±6,b=6代入方程3x²-ax+15-b=0.

解得x=±,这与x∈Z矛盾.

故不存在实数a、b满足条件.

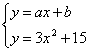解法二:由A∩B≠知方程组有解,

即方程3x²-ax+15-b=0有解.

由(a,b)∈C,得144≥a²+b².

由

消去b,得到关于a的二次不等式

(1+x²)a²-2x(3x²+15)a+［(3x²+15) ²-144］≤0.(*)

∵1+x²＞0且Δ=-36(x²-3) ²＜0(∵x∈Z,∴x²≠3),∴上述不等式(*)没有实数解.

故满足条件的a、b不存在.