题目内容
观察(x2)′＝2x，(x4)′＝4x3，(cos x)′＝－sin x，由归纳推理可得：若定义在R上的函数f(x)满足f(－x)＝f(x)，记g(x)为f(x)的导函数，则g(－x)等于 ( )
| A．f(x) | B．－f(x) | C．g(x) | D．－g(x) |
D
解析
练习册系列答案
相关题目
已知
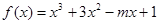在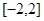
为单调增函数，则实数
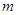的取值范围为（ ）
A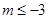． | B． | C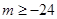． | D． |
设函数
是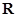
上以4为周期的可导偶函数，则曲线
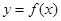在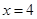
处的切线的斜率为（ ）
A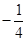． | B． | C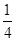． | D．4 |
定积分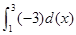
等于( )
| A．－6 | B．6 | C．－3 | D．3 |
函数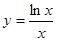
的最大值为（ ）
A． | B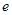． | C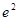． | D． |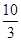
已知
是可导的函数，且
对于
恒成立，则( )
A． |
B． |
C． |
D． |
函数y=x2cosx的导数为（ ）
| A．y′=x2cosx-2xsinx | B．y′=2xcosx+x2sinx |
| C．y′=2xcosx-x2sinx | D．y′=xcosx-x2sinx |
由曲线
，直线
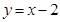及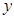
轴所围成的图形的面积为
A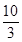． | B．4 | C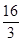． | D．6 |
若a＞0，b＞0，且函数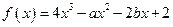
处有极值，则ab的最大值等于( )．
| A．2 | B．3 | C．6 | D．9 |