题目内容
满足条件
的集合
的个数是 （ ）
| A．4 | B．3 | C．2 | D．1 |
C
解析试题分析：因为,所以集合M中一定得有元素2,3.但可以有元素1,也可以没有元素1,因而满足条件的集合M有2个.分别为M={1,2,3},{2,3}.
考点：本小题考查了集合之间的运算关系，主要考查求交集运算.
点评：集合之间的运算关系有三种：一是求并集：
二是求交集：
三是求补集：
.
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知集合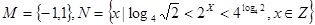 
，则
（ ）
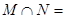A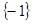． | B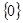． | C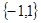． | D． |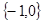
已知集合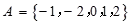
,
,
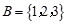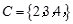,则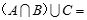
A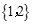． | B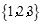． | C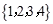． | D． |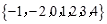
已知全集
，
，则
＝（ ）
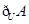A． | B． | C． | D．{ } |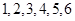
已知集合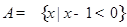
，
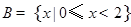，那么
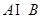等于（ ）
A． | B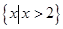． | C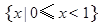． | D． |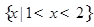
已知集合
，
，则
为 （ ）.
A． | B． | C． | D．  |
已知集合
，
则
（ ）
A．（? ，?1） | B．（?1，? ） | C．（?，3） | D．(3，+) |
若集合
，
，则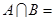
A． | B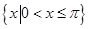． | C． | D． |
已知集合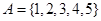
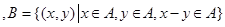,则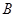
中所含元素的个数为 （ ）
| A．3 | B．6 | C．8 | D．10 |