题目内容
已知椭圆 过点
过点 ,且离心率e=
,且离心率e= .
.
(Ⅰ)求椭圆方程;
(Ⅱ)若直线l:y=kx+m(k≠0)与椭圆交于不同的两点M、N,且线段MN的垂直平分线过定点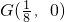 ,求k的取值范围.
,求k的取值范围.
解:(Ⅰ)由题意椭圆的离心率∴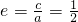 ∴a=2c∴b2=a2-c2=3c2
∴a=2c∴b2=a2-c2=3c2
∴椭圆方程为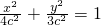 又点
又点 在椭圆上∴
在椭圆上∴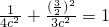 ∴c2=1
∴c2=1
∴椭圆的方程为 …(4分)
…(4分)
(Ⅱ)设M(x1,y1),N(x2,y2)由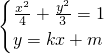
消去y并整理得(3+4k2)x2+8kmx+4m2-12=0…(6分)
∵直线y=kx+m与椭圆有 两个交点△=(8km)2-4(3+4k2)(4m2-12)>0,即m2<4k2+3…(8分)
又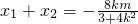 ∴MN中点P的坐标为
∴MN中点P的坐标为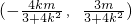 …(9分)
…(9分)
设MN的垂直平分线l'方程: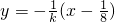
∵p在l'上∴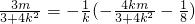 即4k2+8km+3=0
即4k2+8km+3=0
∴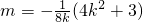 …(11分)
…(11分)
将上式代入得
∴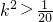
即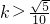 或
或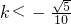 ,∴k的取值范围为
,∴k的取值范围为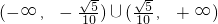
分析:(Ⅰ)由题意知椭圆的离心率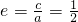 ,故椭圆方程为
,故椭圆方程为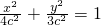 ,又点
,又点 在椭圆上,由此能导出椭圆的方程.
在椭圆上,由此能导出椭圆的方程.
(Ⅱ)设M(x1,y1),N(x2,y2),由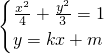 ,消去y并整理得(3+4k2)x2+8kmx+4m2-12=0,由直线y=kx+m与椭圆有两个交点,知m2<4k2+3.又
,消去y并整理得(3+4k2)x2+8kmx+4m2-12=0,由直线y=kx+m与椭圆有两个交点,知m2<4k2+3.又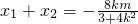 ,知MN中点P的坐标为
,知MN中点P的坐标为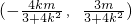 ,由此能求出k的范围.
,由此能求出k的范围.
点评:本题考查椭圆方程和k的取值范围,解题时要认真审题,仔细解答,注意椭圆的灵活运用,合理地进行等价转化.
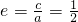 ∴a=2c∴b2=a2-c2=3c2
∴a=2c∴b2=a2-c2=3c2∴椭圆方程为
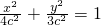 又点
又点 在椭圆上∴
在椭圆上∴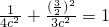 ∴c2=1
∴c2=1∴椭圆的方程为
 …(4分)
…(4分)(Ⅱ)设M(x1,y1),N(x2,y2)由
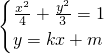
消去y并整理得(3+4k2)x2+8kmx+4m2-12=0…(6分)
∵直线y=kx+m与椭圆有 两个交点△=(8km)2-4(3+4k2)(4m2-12)>0,即m2<4k2+3…(8分)
又
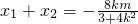 ∴MN中点P的坐标为
∴MN中点P的坐标为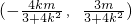 …(9分)
…(9分)设MN的垂直平分线l'方程:
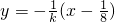
∵p在l'上∴
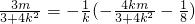 即4k2+8km+3=0
即4k2+8km+3=0∴
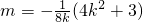 …(11分)
…(11分)将上式代入得

∴
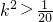
即
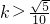 或
或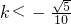 ,∴k的取值范围为
,∴k的取值范围为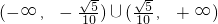
分析:(Ⅰ)由题意知椭圆的离心率
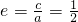 ,故椭圆方程为
,故椭圆方程为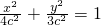 ,又点
,又点 在椭圆上,由此能导出椭圆的方程.
在椭圆上,由此能导出椭圆的方程.(Ⅱ)设M(x1,y1),N(x2,y2),由
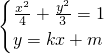 ,消去y并整理得(3+4k2)x2+8kmx+4m2-12=0,由直线y=kx+m与椭圆有两个交点,知m2<4k2+3.又
,消去y并整理得(3+4k2)x2+8kmx+4m2-12=0,由直线y=kx+m与椭圆有两个交点,知m2<4k2+3.又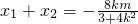 ,知MN中点P的坐标为
,知MN中点P的坐标为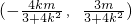 ,由此能求出k的范围.
,由此能求出k的范围.点评:本题考查椭圆方程和k的取值范围,解题时要认真审题,仔细解答,注意椭圆的灵活运用,合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).