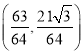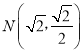Question

【题目】某航运公司用300万元买回客船一艘，此船投入营运后，毎月需开支燃油费、维修费、员工工资，已知每月燃油费7000元，第个月的维修费和工资支出为元.

（1）设月平均消耗为元，求与（月）的函数关系；

（2）投入营运第几个月，成本最低？（月平均消耗最小）

（3）若第一年纯收入50万元（已扣除消耗），以后每年纯收入以5%递减，则多少年后可收回成本？

Answer 1

【答案】（1）；（2）投入第个月，成本最低；

（3）7年后收回成本.

【解析】

（1）先求出购船费和所有支出的和，然后把购船费和所有支出费用平摊到每一个月，即可求得平均消耗与（月）的函数关系；

（2）利用基本不等式可得最值，从而求出此时的值，即可求解；

（3）假设年后可收回成本，则收入是首项为50，公比为0.95的等比数列，然后建立收入大于成本的不等式，即可求解.

（1）购船费和所有支出费为

元，

所以月平均消耗，

即月平均消耗为与的函数关系.

（2）由（1），

当且仅当，即时等号成立，

所以当投入营运100个月时，营运成本最低.

（3）假设年后可收回成本，则收入为：

，

解得时满足条件，时不满足条件，

故7年后可收回成本.