题目内容
若函数f(x)=x- +b恰有两个零点,则b的取值范围是________.
+b恰有两个零点,则b的取值范围是________.
[1,
分析:由f(x)=x- +b=0得x+b=
+b=0得x+b= ,设函数y=x+b,y=
,设函数y=x+b,y= ,然后利用数形结合的思想确定b的取值范围.
,然后利用数形结合的思想确定b的取值范围.
解答: 解:由f(x)=x-
解:由f(x)=x- +b=0得x-b=
+b=0得x-b= ,
,
所以设函数y=f(x)=x+b,y=g(x)= ,
,
则函数g(x)= 的轨迹为半径为1的圆(上半部分).
的轨迹为半径为1的圆(上半部分).
由图象可知,当直线y=x+b经过点(0,1)时,此时两个函数有两个交点,所以此时b=1.
当直线在第二象限与圆相切时,有圆心(0,0)到直线x-y+b=0的距离 ,
,
解得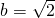 或b=
或b= .
.
由图象可知此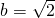 .
.
所以要使函数f(x)=x- +b恰有两个零点,
+b恰有两个零点,
则1 .
.
所以b的取值范围是[1,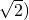 .
.
故答案为:[1,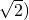 .
.
点评:本题主要考查了函数零点的应用,利用数形结合将零点问题转化为直线与圆的位置关系是解决本题的关键.

分析:由f(x)=x-
 +b=0得x+b=
+b=0得x+b= ,设函数y=x+b,y=
,设函数y=x+b,y= ,然后利用数形结合的思想确定b的取值范围.
,然后利用数形结合的思想确定b的取值范围.解答:
 解:由f(x)=x-
解:由f(x)=x- +b=0得x-b=
+b=0得x-b= ,
,所以设函数y=f(x)=x+b,y=g(x)=
 ,
,则函数g(x)=
 的轨迹为半径为1的圆(上半部分).
的轨迹为半径为1的圆(上半部分).由图象可知,当直线y=x+b经过点(0,1)时,此时两个函数有两个交点,所以此时b=1.
当直线在第二象限与圆相切时,有圆心(0,0)到直线x-y+b=0的距离
 ,
,解得
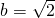 或b=
或b= .
.由图象可知此
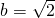 .
.所以要使函数f(x)=x-
 +b恰有两个零点,
+b恰有两个零点,则1
 .
.所以b的取值范围是[1,
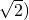 .
.故答案为:[1,
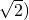 .
.点评:本题主要考查了函数零点的应用,利用数形结合将零点问题转化为直线与圆的位置关系是解决本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
若函数f(x)(x∈R)为奇函数,且存在反函数f-1(x)(与f(x)不同),F(x)=
,则下列关于函数F(x)的奇偶性的说法中正确的是( )
| 2f(x)-2f-1(x) |
| 2f(x)+2f-1(x) |
| A、F(x)是奇函数非偶函数 |
| B、F(x)是偶函数非奇函数 |
| C、F(x)既是奇函数又是偶函数 |
| D、F(x)既非奇函数又非偶函数 |