题目内容
已知函数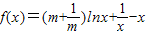 ,(其中常数m>0)
,(其中常数m>0)(1)当m=2时,求f(x)的极大值;
(2)试讨论f(x)在区间(0,1)上的单调性;
(3)当m∈[3,+∞)时,曲线y=f(x)上总存在相异两点P(x1,f(x1))、Q(x2,f(x2)),使得曲线y=f(x)在点P、Q处的切线互相平行,求x1+x2的取值范围.
【答案】分析:(1)利用导数,我们可以确定函数的单调性,这样就可求f(x)的极大值;
(2)求导数,再进行类讨论,利用导数的正负,确定函数的单调性;
(3)曲线y=f(x)在点P、Q处的切线互相平行,意味着导数值相等,由此作为解题的突破口即可.
解答:解:(1)当m=2时,
 (x>0)
(x>0)
令f'(x)<0,可得 或x>2;令f'(x)>0,可得
或x>2;令f'(x)>0,可得 ,
,
∴f(x)在 和(2,+∞)上单调递减,在
和(2,+∞)上单调递减,在 单调递减
单调递减
故
(2) (x>0,m>0)
(x>0,m>0)
①当0<m<1时,则 ,故x∈(0,m)∪
,故x∈(0,m)∪ 时,f′(x)<0;x∈(m,
时,f′(x)<0;x∈(m, )时,f'(x)>0
)时,f'(x)>0
此时f(x)在(0,m), 上单调递减,在(m,
上单调递减,在(m, )单调递增;
)单调递增;
②当m=1时,则 ,故x∈(0,1),有
,故x∈(0,1),有 恒成立,
恒成立,
此时f(x)在(0,1)上单调递减;
③当m>1时,则 ,
,
故 ∪(m,1)时,f'(x)<0;
∪(m,1)时,f'(x)<0; 时,f'(x)>0
时,f'(x)>0
此时f(x)在 ,(m,1)上单调递减,在
,(m,1)上单调递减,在 单调递增
单调递增
(3)由题意,可得f′(x1)=f′(x2)(x1,x2>0,且x1≠x2)
即 ⇒
⇒
∵x1≠x2,由不等式性质可得 恒成立,又x1,x2,m>0
恒成立,又x1,x2,m>0
∴ ⇒
⇒ 对m∈[3,+∞)恒成立
对m∈[3,+∞)恒成立
令 ,则
,则 对m∈[3,+∞)恒成立
对m∈[3,+∞)恒成立
∴g(m)在[3,+∞)上单调递增,∴
故
从而“ 对m∈[3,+∞)恒成立”等价于“
对m∈[3,+∞)恒成立”等价于“ ”
”
∴x1+x2的取值范围为
点评:运用导数,我们可解决曲线的切线问题,函数的单调性、极值与最值,正确求导是我们解题的关键
(2)求导数,再进行类讨论,利用导数的正负,确定函数的单调性;
(3)曲线y=f(x)在点P、Q处的切线互相平行,意味着导数值相等,由此作为解题的突破口即可.
解答:解:(1)当m=2时,

 (x>0)
(x>0)令f'(x)<0,可得
 或x>2;令f'(x)>0,可得
或x>2;令f'(x)>0,可得 ,
,∴f(x)在
 和(2,+∞)上单调递减,在
和(2,+∞)上单调递减,在 单调递减
单调递减 故

(2)
 (x>0,m>0)
(x>0,m>0)①当0<m<1时,则
 ,故x∈(0,m)∪
,故x∈(0,m)∪ 时,f′(x)<0;x∈(m,
时,f′(x)<0;x∈(m, )时,f'(x)>0
)时,f'(x)>0此时f(x)在(0,m),
 上单调递减,在(m,
上单调递减,在(m, )单调递增;
)单调递增; ②当m=1时,则
 ,故x∈(0,1),有
,故x∈(0,1),有 恒成立,
恒成立,此时f(x)在(0,1)上单调递减;
③当m>1时,则
 ,
,故
 ∪(m,1)时,f'(x)<0;
∪(m,1)时,f'(x)<0; 时,f'(x)>0
时,f'(x)>0此时f(x)在
 ,(m,1)上单调递减,在
,(m,1)上单调递减,在 单调递增
单调递增 (3)由题意,可得f′(x1)=f′(x2)(x1,x2>0,且x1≠x2)
即
 ⇒
⇒
∵x1≠x2,由不等式性质可得
 恒成立,又x1,x2,m>0
恒成立,又x1,x2,m>0∴
 ⇒
⇒ 对m∈[3,+∞)恒成立
对m∈[3,+∞)恒成立 令
 ,则
,则 对m∈[3,+∞)恒成立
对m∈[3,+∞)恒成立∴g(m)在[3,+∞)上单调递增,∴

故

从而“
 对m∈[3,+∞)恒成立”等价于“
对m∈[3,+∞)恒成立”等价于“ ”
”∴x1+x2的取值范围为

点评:运用导数,我们可解决曲线的切线问题,函数的单调性、极值与最值,正确求导是我们解题的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
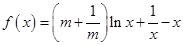 ,(其中常数
,(其中常数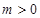 ).
).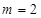 时,求
时,求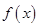 的极大值;
的极大值;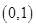 上的单调性;
上的单调性;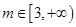 时,曲线
时,曲线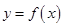 上总存在相异两点
上总存在相异两点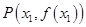 、
、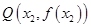 ,使得曲线
,使得曲线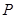 、
、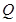 处的切线互相平行,求
处的切线互相平行,求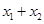 的取值范围.
的取值范围. 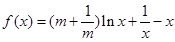 ,(其中常数
,(其中常数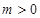 )
)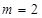 时,求
时,求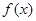 的极大值;
的极大值;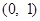 上的单调性;
上的单调性;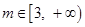 时,曲线
时,曲线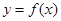 上总存在相异两点
上总存在相异两点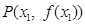 、
、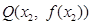 ,使得曲线
,使得曲线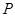 、
、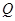 处的切线互相平行,求
处的切线互相平行,求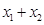 的取值范围.
的取值范围. 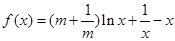 ,(其中常数
,(其中常数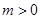 )
)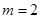 时,求
时,求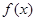 的极大值;
的极大值;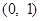 上的单调性;
上的单调性; 时,曲线
时,曲线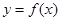 上总存在相异两点
上总存在相异两点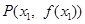 、
、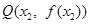 ,使得曲线
,使得曲线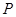 、
、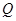 处的切线互相平行,求
处的切线互相平行,求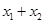 的取值范围.
的取值范围.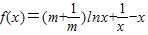 ,(其中常数m>0)
,(其中常数m>0)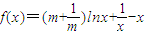 ,(其中常数m>0)
,(其中常数m>0)