题目内容
在直三棱柱ABC-A1B1C1中,AB=BC=| 2 |
分析:由题意,题中E、F分别在AA1、C1B1上,所以“展开”后的图形中必须有AA1、C1B1,画出图形,分类求出结果,找出最短路径.
解答:解:题中E、F分别在AA1、C1B1上,所以“展开”后的图形中必须有AA1、C1B1;故“展开”方式有以下四种:
(ⅰ)沿CC1将面ACC1A1和面BCC1B1展开至同一平面,如图1,求得:EF2=
+2
;
(ⅱ)沿BB1将面ABB1A1和面BCC1B1展开至同一平面,如图2,求得:EF2=
+2
;
(ⅲ)沿A1B1将面ABB1A1和面A1B1C1展开至同一平面,如图3,求得:EF2=
+
;
(ⅳ)沿A1C1将面ACC1A1和面A1C1B1展开至同一平面,如图4,求得:EF2=
;
比较可得(ⅳ)情况下,EF的值最小;
故EF的最小值为
.
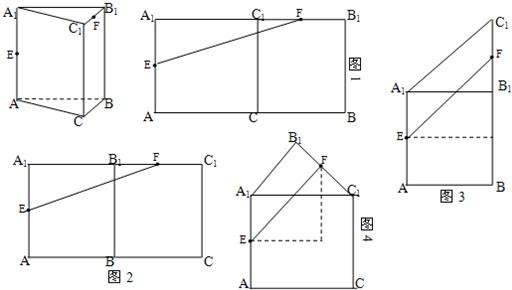
(ⅰ)沿CC1将面ACC1A1和面BCC1B1展开至同一平面,如图1,求得:EF2=
| 11 |
| 2 |
| 2 |
(ⅱ)沿BB1将面ABB1A1和面BCC1B1展开至同一平面,如图2,求得:EF2=
| 7 |
| 2 |
| 2 |
(ⅲ)沿A1B1将面ABB1A1和面A1B1C1展开至同一平面,如图3,求得:EF2=
| 7 |
| 2 |
| 2 |
(ⅳ)沿A1C1将面ACC1A1和面A1C1B1展开至同一平面,如图4,求得:EF2=
| 9 |
| 2 |
比较可得(ⅳ)情况下,EF的值最小;
故EF的最小值为
3
| ||
| 2 |

点评:本题考查棱柱的结构特征,几何体的展开图形,分类讨论思想,是基础题.

练习册系列答案
相关题目
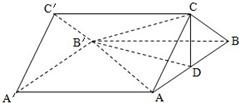 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点. (2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a,
(2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a, 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数). 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,