题目内容
设a为实数,设函数 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t= ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足 的所有实数a
的所有实数a
【答案】
(Ⅰ)m(t)=a(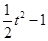 )+t=
)+t=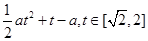
(Ⅱ)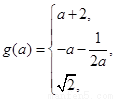

(Ⅲ)满足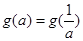 的所有实数a为
的所有实数a为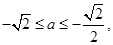 或a=1
或a=1
【解析】解:(Ⅰ)令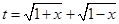
要使有t意义,必须1+x≥0且1-x≥0,即-1≤x≤1,
∴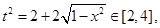 t≥0
①
t≥0
①
t的取值范围是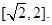 由①得
由①得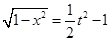
∴m(t)=a(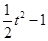 )+t=
)+t=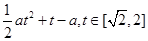
(Ⅱ)由题意知g(a)即为函数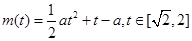 的最大值。
的最大值。
注意到直线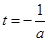 是抛物线
是抛物线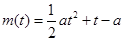 的对称轴,分以下几种情况讨论。
的对称轴,分以下几种情况讨论。
(1)当a>0时,函数y=m(t), 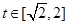 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由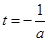 <0知m(t)在
<0知m(t)在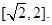 上单调递增,∴g(a)=m(2)=a+2
上单调递增,∴g(a)=m(2)=a+2
(2)当a=0时,m(t)=t, 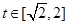 ,∴g(a)=2.
,∴g(a)=2.
(3)当a<0时,函数y=m(t), 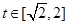 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若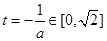 ,即
,即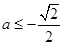 则
则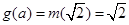
若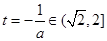 ,即
,即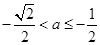 则
则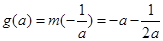
若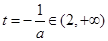 ,即
,即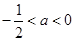 则
则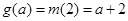
综上有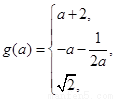
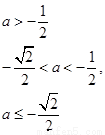
(III)
情形1:当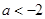 时
时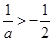 ,此时
,此时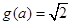 ,
,
由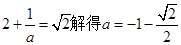 ,与a<-2矛盾。
,与a<-2矛盾。
情形2:当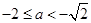
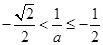 时,此时
时,此时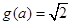 ,
,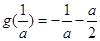
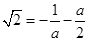 解得,
解得, 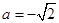 与
与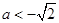 矛盾。
矛盾。
情形3:当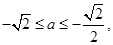
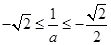 时,此时
时,此时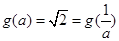
所以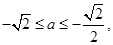
情形4:当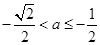 时,
时,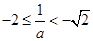 ,此时
,此时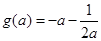 ,
,
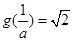
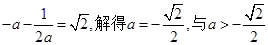 矛盾。
矛盾。
情形5:当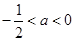 时,
时,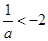 ,此时g(a)=a+2,
,此时g(a)=a+2, 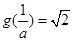
由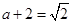 解得
解得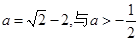 矛盾。
矛盾。
情形6:当a>0时,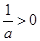 ,此时g(a)=a+2,
,此时g(a)=a+2, 
由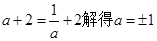 ,由a>0得a=1.
,由a>0得a=1.
综上知,满足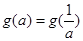 的所有实数a为
的所有实数a为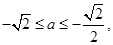 或a=1
或a=1

练习册系列答案
相关题目
 的最大值为g(a).
的最大值为g(a). ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t) 的所有实数a
的所有实数a 的最大值为g(a).
的最大值为g(a). ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t); 的最大值为g(a)。
的最大值为g(a)。 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t) 的所有实数a
的所有实数a 的最大值为g(a)。
的最大值为g(a)。 ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t); 的所有实数a。
的所有实数a。