题目内容
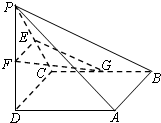 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点.(1)求证:GC⊥平面PEF;
(2)求证:PA∥平面EFG;
(3)求三棱锥P-EFG的体积.
分析:(1):因为PD⊥平面ABCD,GC?平面ABCD,所以GC⊥PD.因为GC⊥CD且PD∩CD=D所以GC⊥平面PCD.
(2)因为EF∥CD且EF∥GH所以E,F,H,G四点共面.又因为F,H分别为DP,DA的中点所以PA∥FH因为PA?平面EFG,FH?平面EFG,所以PA∥平面EFG.
(3)先求出底面的面积S△PEF=
EF×PF=
,由题意得GC=
BC=1所以三棱锥的体积为VP-EFG=VG-PEF=
S△PEF•GC=
.
(2)因为EF∥CD且EF∥GH所以E,F,H,G四点共面.又因为F,H分别为DP,DA的中点所以PA∥FH因为PA?平面EFG,FH?平面EFG,所以PA∥平面EFG.
(3)先求出底面的面积S△PEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
解答:(1)证明:∵PD⊥平面ABCD,GC?平面ABCD,
∴GC⊥PD.
∵ABCD为正方形,∴GC⊥CD.∵PD∩CD=D,
∴GC⊥平面PCD.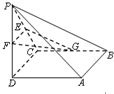
(2)证明:如图,取AD的中点H,连接GH,FH,
∵E,F分别为PC,PD的中点,
∴EF∥CD.
∵G,H分别为BC,AD的中点,
∴GH∥CD.
∴EF∥GH.
∴E,F,H,G四点共面.
∵F,H分别为DP,DA的中点,
∴PA∥FH.
∵PA?平面EFG,FH?平面EFG,
∴PA∥平面EFG.
(3)解:∵PF=
PD=1,EF=
CD=1,
∴S△PEF=
EF×PF=
.
∵GC=
BC=1,
∴VP-EFG=VG-PEF=
S△PEF•GC=
×
×1=
.
∴GC⊥PD.
∵ABCD为正方形,∴GC⊥CD.∵PD∩CD=D,
∴GC⊥平面PCD.

(2)证明:如图,取AD的中点H,连接GH,FH,
∵E,F分别为PC,PD的中点,
∴EF∥CD.
∵G,H分别为BC,AD的中点,
∴GH∥CD.
∴EF∥GH.
∴E,F,H,G四点共面.
∵F,H分别为DP,DA的中点,
∴PA∥FH.
∵PA?平面EFG,FH?平面EFG,
∴PA∥平面EFG.
(3)解:∵PF=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△PEF=
| 1 |
| 2 |
| 1 |
| 2 |
∵GC=
| 1 |
| 2 |
∴VP-EFG=VG-PEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:证明线面垂直关键是证明直线与面内的两条相交直线垂直;证明线面平行关键是证明已知直线与面内一条直线平行即可;求三棱锥的体积时有时需要换一个底面积与高都好求的顶点,在利用体积公式求出体积即可.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.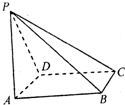 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,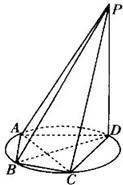 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.