题目内容
（2013•楚雄州模拟）已知椭圆
+
=1（a＞b＞0）的一个顶点为B（0，4），离心率e=
，直线l交椭圆于M、N两点．
（1）若直线l的方程为y=x-4，求弦MN的长；
（2）如果△BMN的重心恰好为椭圆的右焦点F，求直线l方程的一般式．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 5 |
（1）若直线l的方程为y=x-4，求弦MN的长；
（2）如果△BMN的重心恰好为椭圆的右焦点F，求直线l方程的一般式．
分析：（1）由已知中椭圆
+
=1（a＞b＞0）的一个顶点为B（0，4），离心率e=
，根据e=
，b=4，a2=b2+c2可求出椭圆的标准方程，进而求直线l的方程及弦长公式，得到弦MN的长；
（2）设线段MN的中点为Q（x0，y0），结合（1）中结论，及△BMN的重心恰好为椭圆的右焦点F，由重心坐标公式，可得Q点坐标，由中点公式及M，N也在椭圆上，求出MN的斜率，可得直线l方程．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 5 |
| c |
| a |
（2）设线段MN的中点为Q（x0，y0），结合（1）中结论，及△BMN的重心恰好为椭圆的右焦点F，由重心坐标公式，可得Q点坐标，由中点公式及M，N也在椭圆上，求出MN的斜率，可得直线l方程．
解答：
解：（1）由已知椭圆
+
=1（a＞b＞0）的一个顶点为B（0，4），
∴b=4，
又∵离心率e=
=
，
即
=
，
∴
=
，解得a2=20，
∴椭圆方程为
+
=1； …（3分）
由4x2+5y2=80与y=x-4联立，
消去y得9x2-40x=0，
∴x1=0，x2=
，
∴所求弦长|MN|=
|x2-x1|=
； …（6分）
（2）椭圆右焦点F的坐标为（2，0），
设线段MN的中点为Q（x0，y0），
由三角形重心的性质知
=2
，又B（0，4），
∴（2．-4）=2（x0-2，y0），
故得x0=3，y0=-2，
求得Q的坐标为（3，-2）； …（9分）
设M（x1，y1），N（x2，y2），则x1+x2=6，y1+y2=-4，
且
+
=1，
+
=1，…（11分）
以上两式相减得
+
=0，
∴kMN=
=-
•
=-
•
=
，
故直线MN的方程为y+2=
(x-3)，即6x-5y-28=0． …（13分）
解：（1）由已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
∴b=4，
又∵离心率e=
| c |
| a |
| ||
| 5 |
即
| c2 |
| a2 |
| 1 |
| 5 |
∴
| a2-b2 |
| a2 |
| 1 |
| 5 |
∴椭圆方程为
| x2 |
| 20 |
| y2 |
| 16 |
由4x2+5y2=80与y=x-4联立，
消去y得9x2-40x=0，
∴x1=0，x2=
| 40 |
| 9 |
∴所求弦长|MN|=
| 1+12 |
40
| ||
| 9 |
（2）椭圆右焦点F的坐标为（2，0），
设线段MN的中点为Q（x0，y0），
由三角形重心的性质知
| BF |
| FQ |
∴（2．-4）=2（x0-2，y0），
故得x0=3，y0=-2，
求得Q的坐标为（3，-2）； …（9分）
设M（x1，y1），N（x2，y2），则x1+x2=6，y1+y2=-4，
且
| ||
| 20 |
| ||
| 16 |
| ||
| 20 |
| ||
| 16 |
以上两式相减得
| (x1+x2)(x1-x2) |
| 20 |
| (y1+y2)(y1-y2) |
| 16 |
∴kMN=
| y1-y2 |
| x1-x2 |
| 4 |
| 5 |
| x1+x2 |
| y1+y2 |
| 4 |
| 5 |
| 6 |
| -4 |
| 6 |
| 5 |
故直线MN的方程为y+2=
| 6 |
| 5 |
点评：本题考查的知识点是直线的一般方程，直线与圆锥曲线，熟练掌握椭圆的简单性质是重心坐标，中点公式等基本公式，是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
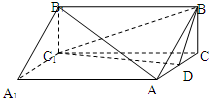（2013•楚雄州模拟）如图，三棱柱ABC-A1B1C1中，AA1⊥面ABC，BC⊥AC，AC=BC=2，AA1=3，D为AC的中点．