题目内容
(2012•汕头一模)如果△ABC不是直角三角形,且A、B、C是△ABC的三个内角:
(1)求证:tanA+tanB+tanC=tanA•tanB•tanC
(2)如果sinA=
,cosB=
,求cosC.
(1)求证:tanA+tanB+tanC=tanA•tanB•tanC
(2)如果sinA=
| 4 |
| 5 |
| 12 |
| 13 |
分析:(1)利用和角的正切公式,结合三角形的内角和,即可证得结论;
(2)先求出cosA,再利用和角的余弦公式,即可求得cosC.
(2)先求出cosA,再利用和角的余弦公式,即可求得cosC.
解答:(1)证明:由题意知:A≠
,B≠
,C≠
,且A+B+C=π
∴tan(A+B)=tan(π-C)=-tanC….…(1分)
又∵tan(A+B)=
….…(2分)
∴tanA+tanB=tan(A+B)(1-tanAtanB)=-tanC(1-tanAtanB)=-tanC+tanAtanBtanC….…(4分)
即tanA+tanB+tanC=tanAtanBtanC….…(5分)
(2)解:由cosB=
>0知道:B∈(0,
),
∵sin2B+cos2B=1,∴sinB=
….…(6分)
而sinA>sinB,∴A>B
①当A∈(0,
)时,cosA=
…(7分)
∴cosC=-cos(A+B)=sinAsinB-cosAcosB=
×
-
×
=-
….…(9分)
②当A∈(
,π)时,cosA=-
….…(10分)
∴cosC=-cos(A+B)=sinAsinB-cosAcosB=
×
-(-
)×
=
…(12分)
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴tan(A+B)=tan(π-C)=-tanC….…(1分)
又∵tan(A+B)=
| tanA+tanB |
| 1-tanAtanB |
∴tanA+tanB=tan(A+B)(1-tanAtanB)=-tanC(1-tanAtanB)=-tanC+tanAtanBtanC….…(4分)
即tanA+tanB+tanC=tanAtanBtanC….…(5分)
(2)解:由cosB=
| 12 |
| 13 |
| π |
| 2 |
∵sin2B+cos2B=1,∴sinB=
| 5 |
| 13 |
而sinA>sinB,∴A>B
①当A∈(0,
| π |
| 2 |
| 3 |
| 5 |
∴cosC=-cos(A+B)=sinAsinB-cosAcosB=
| 4 |
| 5 |
| 5 |
| 13 |
| 3 |
| 5 |
| 2 |
| 13 |
| 16 |
| 65 |
②当A∈(
| π |
| 2 |
| 3 |
| 5 |
∴cosC=-cos(A+B)=sinAsinB-cosAcosB=
| 4 |
| 5 |
| 5 |
| 13 |
| 3 |
| 5 |
| 2 |
| 13 |
| 56 |
| 65 |
点评:本题考查和角的正切公式与余弦公式,考查分类讨论的数学思想,考查学生的计算能力,正确运用公式是关键,属于中档题.

练习册系列答案
相关题目
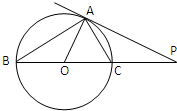 (2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为
(2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为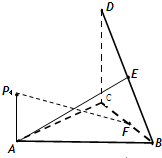 (2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
(2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.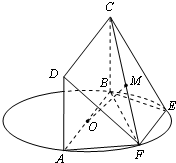 (2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.