题目内容
若{an}是等差数列,m,n,p是互不相等的正整数,则有正确的结论:m(ap-an)+n(am-ap)+p(an-am)=0;若{bn}是等比数列,m,n,p是互不相等的正整数,则有正确的结论:________.
(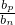 )m•(
)m•( )n•(
)n•(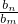 )p=1
)p=1
分析:仔细分析题干中给出的不等式的结论:m(ap-an)+n(am-ap)+p(an-am)=0的规律,结合等差数列与等比数列具有类比性,且等差数列与和差有关,等比数列与积商有关,因此等比数列类比到等差数列的:(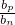 )m•(
)m•(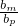 )n•(
)n•(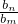 )p=1成立.
)p=1成立.
解答:等差数列中的m(ap-an)可以类比等比数列中的(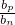 )m
)m
等差数列中的n(am-ap)可以类比等比数列中的(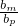 )n
)n
等差数列中的p(an-am)可以类比等比数列中的(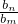 )p
)p
等差数列中的“加”可以类比等比数列中的“乘”,等差数列中的“乘”可以类比等比数列中的“乘方”.
故有:(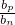 )m•(
)m•(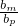 )n•(
)n•(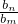 )p=1.
)p=1.
故答案为:(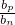 )m•(
)m•(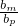 )n•(
)n•(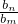 )p=1.
)p=1.
点评:本题主要考查等差数列类比到等比数列的类比推理,类比推理一般步骤:①找出等差数列、等比数列之间的相似性或者一致性.②用等差数列的性质去推测物等比数列的性质,得出一个明确的命题(或猜想).
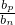 )m•(
)m•( )n•(
)n•(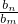 )p=1
)p=1分析:仔细分析题干中给出的不等式的结论:m(ap-an)+n(am-ap)+p(an-am)=0的规律,结合等差数列与等比数列具有类比性,且等差数列与和差有关,等比数列与积商有关,因此等比数列类比到等差数列的:(
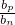 )m•(
)m•(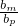 )n•(
)n•(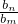 )p=1成立.
)p=1成立.解答:等差数列中的m(ap-an)可以类比等比数列中的(
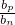 )m
)m等差数列中的n(am-ap)可以类比等比数列中的(
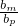 )n
)n等差数列中的p(an-am)可以类比等比数列中的(
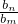 )p
)p等差数列中的“加”可以类比等比数列中的“乘”,等差数列中的“乘”可以类比等比数列中的“乘方”.
故有:(
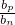 )m•(
)m•(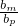 )n•(
)n•(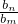 )p=1.
)p=1.故答案为:(
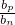 )m•(
)m•(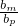 )n•(
)n•(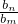 )p=1.
)p=1.点评:本题主要考查等差数列类比到等比数列的类比推理,类比推理一般步骤:①找出等差数列、等比数列之间的相似性或者一致性.②用等差数列的性质去推测物等比数列的性质,得出一个明确的命题(或猜想).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目