题目内容
 (2013•临沂一模)某次考试中,从甲,乙两个班各抽取10名学生的成绩进行统计分析,两班10名学生成绩的茎叶图如图所示,成绩不小于90分为及格.
(2013•临沂一模)某次考试中,从甲,乙两个班各抽取10名学生的成绩进行统计分析,两班10名学生成绩的茎叶图如图所示,成绩不小于90分为及格.(I)从每班抽取的学生中各抽取一人,求至少有一人及格的概率;
(Ⅱ)从甲班l0人中取两人,乙班l0人中取一人,三人中及格人数记为X,求X的分布列和期望.
分析:(I)由茎叶图可知:甲班有4人及格,乙班有5人及格,设事件“从每班10名学生中各抽取一人,至少有一人及格”为A.可先求出其对立事件
的概率,再利用P(A)=1-P(
)即可得出;
(II)由题意可得X的所有可能取值为0,1,2,3.由题意可知:从甲班10人中任选的2人和从乙班10人中任选1人共有
种选法.①X=0表示从甲班选的2人和从乙班所选的1人都不及格,有
种选法;②X=1表示从甲班选的2人和从乙班所选的1人3人中只有1人及格,故有
•
+
种选法;③X=2表示从甲班选的2人和从乙班所选的1人3人中只有2人及格,故有
+
•
种选法;④X=3表示从甲班选的2人和从乙班所选的1人3人都及格,故有
•
种选法.再利用古典概型的概率计算公式、互为对立事件的概率计算公式、相互独立事件的概率计算公式、互斥事件的概率计算公式、随机变量的分布列及其数学期望的计算公式即可得出.
. |
| A |
. |
| A |
(II)由题意可得X的所有可能取值为0,1,2,3.由题意可知:从甲班10人中任选的2人和从乙班10人中任选1人共有
| C | 2 10 |
| C | 1 10 |
| C | 2 6 |
| C | 1 5 |
| C | 1 4 |
| C | 1 6 |
| C | 1 5 |
| C | 2 6 |
| C | 1 5 |
| C | 2 4 |
| C | 1 5 |
| C | 1 4 |
| C | 1 6 |
| C | 1 5 |
| C | 2 4 |
| C | 1 5 |
解答:解:(I)由茎叶图可知:甲班有4人及格,乙班有5人及格,
设事件“从每班10名学生中各抽取一人,至少有一人及格”为A.
则P(
)=
=
,
∴P(A)=1-P(
)=1-
=
.
(II)由题意可得X的所有可能取值为0,1,2,3.
P(X=0)=
=
;P(X=1)=
•
+
•
=
;
P(x=2)=
•
+
•
=
;
P(X=3)=
•
=
.
所以X的分布列为
因此E(X)=0×
+1×
+2×
+3×
=
.
设事件“从每班10名学生中各抽取一人,至少有一人及格”为A.
则P(
. |
| A |
| ||||
|
| 3 |
| 10 |
∴P(A)=1-P(
. |
| A |
| 3 |
| 10 |
| 7 |
| 10 |
(II)由题意可得X的所有可能取值为0,1,2,3.
P(X=0)=
| ||||
|
| 1 |
| 6 |
| ||||
|
| ||
|
| ||
|
| ||
|
| 13 |
| 30 |

P(x=2)=
| ||
|
| ||
|
| ||||
|
| ||
|
| 1 |
| 3 |
P(X=3)=
| ||
|
| ||
|
| 1 |
| 15 |
所以X的分布列为
因此E(X)=0×
| 1 |
| 6 |
| 13 |
| 30 |
| 1 |
| 3 |
| 1 |
| 15 |
| ′13 |
| 10 |
点评:熟练掌握古典概型的概率计算公式、互为对立事件的概率计算公式、相互独立事件的概率计算公式、互斥事件的概率计算公式、随机变量的分布列及其数学期望的计算公式是解题的关键.

练习册系列答案
相关题目
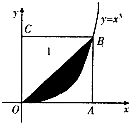 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )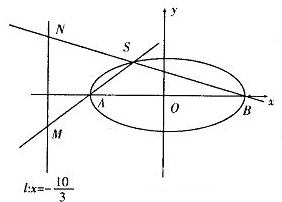 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C: