题目内容
已知函数f(x)=ax3+bx2+(b-a)x(a,b是不同时为零的常数),其导函数为f'(x).(1)当
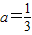 时,若不等式
时,若不等式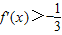 对任意x∈R恒成立,求b的取值范围;
对任意x∈R恒成立,求b的取值范围;(2)求证:函数y=f'(x)在(-1,0)内至少存在一个零点.
【答案】分析:(1)把a= 代入求导后转化为二次不等式恒成立的问题,根据二次不等式对应的二次函数开口方向及二次方程的判别式联立解决;
代入求导后转化为二次不等式恒成立的问题,根据二次不等式对应的二次函数开口方向及二次方程的判别式联立解决;
(2)说明函数y=f'(x)在(-1,0)内至少存在一个零点,只要在区间[-1,0]内找到两个值,使f′(-1)•f′(0)<0即可.
解答:解:(1)当a= 时,f(x)=
时,f(x)=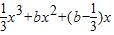 ,
,
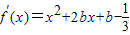 ,
,
要使对任意x∈R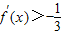 恒成立,即
恒成立,即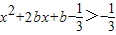 恒成立,
恒成立,
也就是x2+2bx+b>0恒成立,则△=(2b)2-4b<0,解得:0<b<1.
所以不等式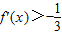 对任意x∈R恒成立的b的取值范围是(0,1);
对任意x∈R恒成立的b的取值范围是(0,1);
(2)令g(x)=f′(x)=3ax2+2bx+b-a,
g(-1)=3a×(-1)2+2b×(-1)+b-a=2a-b,
g(0)=b-a
g(- )=
)=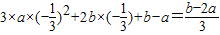 ,
,
所以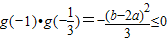 ,
,
上式等号成立时说明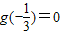 ,也满足至少有一个零点
,也满足至少有一个零点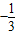 .
.
所以函数y=f'(x)在(-1,0)内至少存在一个零点.
点评:本题主要考查利用导数法研究函数的单调性,函数的图象和性质以及方程的根转化为函数图象的交点解决等问题.
 代入求导后转化为二次不等式恒成立的问题,根据二次不等式对应的二次函数开口方向及二次方程的判别式联立解决;
代入求导后转化为二次不等式恒成立的问题,根据二次不等式对应的二次函数开口方向及二次方程的判别式联立解决;(2)说明函数y=f'(x)在(-1,0)内至少存在一个零点,只要在区间[-1,0]内找到两个值,使f′(-1)•f′(0)<0即可.
解答:解:(1)当a=
 时,f(x)=
时,f(x)=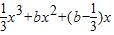 ,
,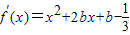 ,
,要使对任意x∈R
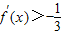 恒成立,即
恒成立,即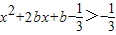 恒成立,
恒成立,也就是x2+2bx+b>0恒成立,则△=(2b)2-4b<0,解得:0<b<1.
所以不等式
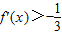 对任意x∈R恒成立的b的取值范围是(0,1);
对任意x∈R恒成立的b的取值范围是(0,1);(2)令g(x)=f′(x)=3ax2+2bx+b-a,
g(-1)=3a×(-1)2+2b×(-1)+b-a=2a-b,
g(0)=b-a
g(-
 )=
)=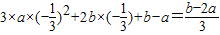 ,
,所以
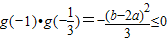 ,
,上式等号成立时说明
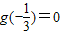 ,也满足至少有一个零点
,也满足至少有一个零点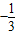 .
.所以函数y=f'(x)在(-1,0)内至少存在一个零点.
点评:本题主要考查利用导数法研究函数的单调性,函数的图象和性质以及方程的根转化为函数图象的交点解决等问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目