题目内容
(本题满分14分)已知以函数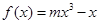 的图象上的点
的图象上的点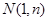 为切点的切线的倾斜角为
为切点的切线的倾斜角为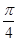 .
.
(1)求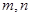 的值;
的值;
(2)是否存在正整数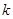 ,使不等式
,使不等式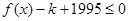 对于
对于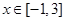 恒成立?若存在,求出最小的正整数
恒成立?若存在,求出最小的正整数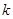 ,若不存在,说明理由;
,若不存在,说明理由;
(3)对于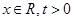 ,比较
,比较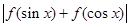 与
与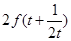 的大小.
的大小.
(1)由 得
得 ,
, …………1分
…………1分
又由题意知 所以
所以 ,解得
,解得 …………2分
…………2分
又点 在函数
在函数 的图象上,所以
的图象上,所以 . …………3分
. …………3分
(2)由(1)知 ,所以
,所以 ,
,
令 得
得 .
…………5分
.
…………5分
在区间 上,
上, 在此区间为增函数,
在此区间为增函数, 时,
时, 在此区间为减函数,
在此区间为减函数, [
[ ,3]时,
,3]时, 在此区间为增函数,
在此区间为增函数,
所以
 处取得极大值
处取得极大值 (-
(- )
) . …………7分
. …………7分
而 ,比较
,比较 (-
(- )和
)和 的大小知道
的大小知道 在区间
在区间 上的最大值为
上的最大值为 ,
…………9分
,
…………9分
(没有说明理由而直接说 最大,扣3分)
最大,扣3分)
所以不等式 对于
对于 恒成立等价于
恒成立等价于 成立,即
成立,即
所以存在满足条件的正整数,且最小的正整数 .
…………10分
.
…………10分
(3)




 .
…………12分
.
…………12分
又
 时,
时, 在此区间为增函数,所以由
在此区间为增函数,所以由 得
得
 . …………13分
. …………13分
所以 时,有
时,有 .
…………14分
.
…………14分
【解析】略

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
