题目内容
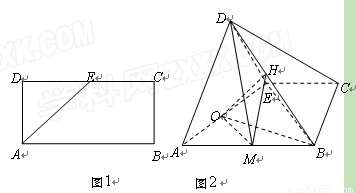
(本小题满分12分)如图1所示,在矩形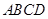 中,
中,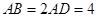 ,
,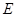 为
为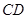 的中点,沿
的中点,沿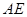 将
将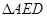 折起,如图2所示,在图2中,
折起,如图2所示,在图2中, 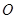 、
、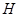 、
、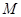 分别为
分别为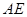 、
、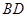 、
、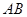 的中点,且
的中点,且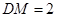 .
.
(Ⅰ)求证: 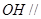 平面
平面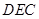 ;
;
(Ⅱ) 求证:面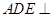 面
面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
【答案】
(Ⅰ) 证明:取 中点
中点 ,连结
,连结 ,在
,在 中,
中, 为中位线
为中位线

所以, 
因为 面
面 ,
, 面
面
所以, 面
面 …………2分
…………2分
同理,底面 中,
中, 面
面
而 且
且 面
面 ,
,
 面
面 所以,面
所以,面 面
面
而 面
面 所以,
所以, 平面
平面 …………4分
…………4分
(Ⅱ) 证明:连结 ,
, ,则
,则
而 ,所以,在
,所以,在 中,
中,
所以, …………6分
…………6分
又 中,
中, ,
, 面
面 ,
, 面
面
所以,  面
面
而
 ,所以, 面
,所以, 面 面
面 …………8分
…………8分
(Ⅲ)解:因为 为
为 中点
中点
所以,  到底面
到底面 的距离等于
的距离等于 …………10分
…………10分
而
所以, …………12分
…………12分
【解析】略

练习册系列答案
相关题目