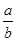题目内容
已知点P是双曲线 右支上一点,F是该双曲线的右焦点,点M为线段PF的中点,若|OM|=3,则点P到该双曲线右准线的距离为( )
右支上一点,F是该双曲线的右焦点,点M为线段PF的中点,若|OM|=3,则点P到该双曲线右准线的距离为( )A.

B.

C.

D.

【答案】分析:根据a2-b2=c2求出右焦点F的坐标,根据双曲线的准线公式x= 求出右准线方程,然后设P的坐标(x,y),代入到双曲线方程,由M为PF的中点,根据中点坐标公式求出M的坐标,利用两点间的距离公式求出
求出右准线方程,然后设P的坐标(x,y),代入到双曲线方程,由M为PF的中点,根据中点坐标公式求出M的坐标,利用两点间的距离公式求出  ,最后联立方程得到x,根据两点间的距离公式求出P到准线方程的距离即可.
,最后联立方程得到x,根据两点间的距离公式求出P到准线方程的距离即可.
解答:解:由双曲线 得a=2,b=
得a=2,b= ,
,
根据勾股定理得c=3,则右准线为 x= ,右焦点F(3,0),
,右焦点F(3,0),
设P(x,y),P在双曲线上,
∴ ①
①
由点M为PF中点,
根据中点坐标公式求得M( ,
, ),
),
且| |=3
|=3
∴ +
+ =9②
=9②
由①②解得:x= .
.
右准线为 x= ,则点P到双曲线右准线的距离是
,则点P到双曲线右准线的距离是  -
- =
= .
.
故选A.
点评:本题是一道综合题,考查学生掌握双曲线的一些简单性质,会利用两点间的距离公式及中点坐标公式、点到直线的距离公式化简求值,同时也考查学生掌握向量的运用法则及向量模的求法,做题时要求学生知识面要宽,综合运用数学知识解决问题.
 求出右准线方程,然后设P的坐标(x,y),代入到双曲线方程,由M为PF的中点,根据中点坐标公式求出M的坐标,利用两点间的距离公式求出
求出右准线方程,然后设P的坐标(x,y),代入到双曲线方程,由M为PF的中点,根据中点坐标公式求出M的坐标,利用两点间的距离公式求出  ,最后联立方程得到x,根据两点间的距离公式求出P到准线方程的距离即可.
,最后联立方程得到x,根据两点间的距离公式求出P到准线方程的距离即可.解答:解:由双曲线
 得a=2,b=
得a=2,b= ,
,根据勾股定理得c=3,则右准线为 x=
 ,右焦点F(3,0),
,右焦点F(3,0),设P(x,y),P在双曲线上,
∴
 ①
①由点M为PF中点,
根据中点坐标公式求得M(
 ,
, ),
),且|
 |=3
|=3∴
 +
+ =9②
=9②由①②解得:x=
 .
.右准线为 x=
 ,则点P到双曲线右准线的距离是
,则点P到双曲线右准线的距离是  -
- =
= .
.故选A.
点评:本题是一道综合题,考查学生掌握双曲线的一些简单性质,会利用两点间的距离公式及中点坐标公式、点到直线的距离公式化简求值,同时也考查学生掌握向量的运用法则及向量模的求法,做题时要求学生知识面要宽,综合运用数学知识解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 右支上一点,
右支上一点, 分别是双曲线的左、右焦点,I为
分别是双曲线的左、右焦点,I为 的内心,若
的内心,若
 成立,则双曲线的离心率为( )
成立,则双曲线的离心率为( ) C.2 D.
C.2 D.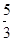
 右支上一点,
右支上一点, ,分别是双曲线的左、右焦点,I为
,分别是双曲线的左、右焦点,I为 的内心,若
的内心,若  成立,则双曲线的离心率为( )
成立,则双曲线的离心率为( ) C.2 D.
C.2 D. [来源:]
[来源:] 右支上一点,
右支上一点, ,分别是双曲线的左、右焦点,I为
,分别是双曲线的左、右焦点,I为 的内心,若
的内心,若  成立,则双曲线的离心率为( )
成立,则双曲线的离心率为( ) C.2 D.
C.2 D.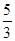
 右支上任意一点,由P点向两条渐近线引垂直,垂足分别为M、N,则△PMN的面积为
右支上任意一点,由P点向两条渐近线引垂直,垂足分别为M、N,则△PMN的面积为  右支上一点,
右支上一点,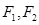 分别为双曲线的左、右焦点,I为△
分别为双曲线的左、右焦点,I为△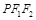 的内心,若
的内心,若 成立,则
成立,则 的值为( )
的值为( )  B.
B. C.
C. D.
D.