题目内容
在以O为坐标原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点.已知|AB|=2|OA|,且点B的纵坐标大于零.
(1)求向量![]() 的坐标;
的坐标;
(2)求圆x2-6y+y2+2y=0关于直线OB对称的圆的方程;
(3)设直线l以![]() 为方向向量且过(0,a)点,问是否存在实数a,使得椭圆
为方向向量且过(0,a)点,问是否存在实数a,使得椭圆![]() 上有两个不同的点关于直线l对称.若不存在,请说明理由;存在请求出实数a的取值范围.
上有两个不同的点关于直线l对称.若不存在,请说明理由;存在请求出实数a的取值范围.
答案:
解析:
解析:
解:(1)设![]() ,则由
,则由 ,可得
,可得
解得![]() 或
或![]() .又
.又![]() ,且
,且![]()
故![]() ,
,![]() 3分
3分
(2)由![]() 可知直线OB的方程为
可知直线OB的方程为![]()
![]() 可知圆心为
可知圆心为![]() ,半径为
,半径为![]() .
.
设圆心关于直线OB的对称点坐标为![]() ,由
,由
解得![]() ,故所求圆的方程为
,故所求圆的方程为![]() 6分
6分
(3)假设椭圆上存在两点![]()
![]() 关于直线
关于直线![]() 对称,设其中点坐标为
对称,设其中点坐标为![]() 由已知直线
由已知直线![]() 的方程为
的方程为![]() ,可设直线AB的方程为
,可设直线AB的方程为![]() 将其与已知椭圆方程联立得
将其与已知椭圆方程联立得![]() .
.
由韦达定理知![]() ,
,![]() .
.
中点![]() 在圆的内部可知
在圆的内部可知
解得![]() .
.
又![]() 在直线
在直线![]() 上,故
上,故![]() ,解得
,解得![]() 代入
代入![]()
解得![]()
即存在满足题意的实数![]() 其取值范围为
其取值范围为![]() 12分
12分

练习册系列答案
相关题目
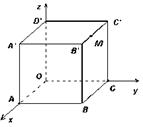
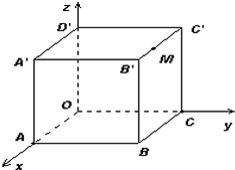 11、如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
11、如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
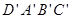 ,点M在
,点M在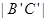 上,且
上,且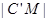
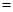 2
2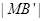 ,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 .
,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 .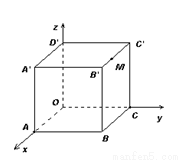
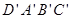 ,点M在
,点M在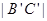 上,且
上,且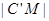
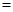 2
2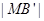 ,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
.
,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
.
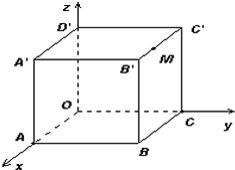 如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 ________.
如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 ________.