题目内容
(2008•海珠区一模)(坐标系与参数方程选作题)圆ρ=2cosθ-2sinθ的圆心与直线ρcosθ=3的距离是
2
2
.分析:由ρ=2cosθ-2sinθ,知(x-1)2+(y+1)2=2,故圆心为(1,-1),由直线ρcosθ=3,知x=3,由此能求出圆ρ=2cosθ-2sinθ的圆心(1,-1)与直线ρcosθ=3的距离.
解答:解:∵ρ=2cosθ-2sinθ,
∴ρ2=2ρcosθ-2ρsinθ,
故x2+y2=2x-2y,
即(x-1)2+(y+1)2=2,
∴圆心为(1,-1),
∵直线ρcosθ=3,
∴x=3,
∴圆ρ=2cosθ-2sinθ的圆心与直线ρcosθ=3的距离,
即为圆(x-1)2+(y+1)2=2的圆心(1,-1))与直线x=3的距离:d=2.
故答案为:2.
∴ρ2=2ρcosθ-2ρsinθ,
故x2+y2=2x-2y,
即(x-1)2+(y+1)2=2,
∴圆心为(1,-1),
∵直线ρcosθ=3,
∴x=3,
∴圆ρ=2cosθ-2sinθ的圆心与直线ρcosθ=3的距离,
即为圆(x-1)2+(y+1)2=2的圆心(1,-1))与直线x=3的距离:d=2.
故答案为:2.
点评:本题考查简单曲线的极坐标方程,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
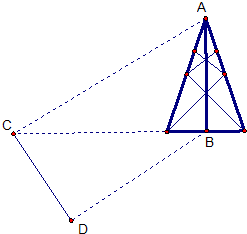 (2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB.
(2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB. (2008•海珠区一模)如果一个几何体的三视图是如图所示(单位长度:cm则此几何体的表面积是( )
(2008•海珠区一模)如果一个几何体的三视图是如图所示(单位长度:cm则此几何体的表面积是( )