题目内容
在区间[0，1]上随机取两个数m，n，则关于函数f（x）=| 4 | 3 |
分析：本题考查的知识点是几何概型的意义，关键是要找出函数f（x）=
mx2-nx+1在[1，+∞）上为增函数时，点（m，n）对应的平面区域面积的大小，及m∈[0，1]，n∈[0，1]时，点（m，n）对应的平面区域面积的大小，并将它们代入几何概型计算公式进行解答．
| 4 |
| 3 |
解答：
解：∵函数f（x）=
mx2-nx+1
∴y'=4mx2-n，
若函数f（x）=
mx2-nx+1在[1，+∝）上为增函数
则y'=4mx2-n≥0在[1，+∝）上恒成立，
即4m-n≥0，其对应的平面区域如下图中阴影所示：
则函数y=
mx3-nx+1在[1，+∝）上为增函数的概率P=
=
=
故答案为：
．
解：∵函数f（x）=| 4 |
| 3 |
∴y'=4mx2-n，
若函数f（x）=
| 4 |
| 3 |
则y'=4mx2-n≥0在[1，+∝）上恒成立，
即4m-n≥0，其对应的平面区域如下图中阴影所示：
则函数y=
| 2 |
| 3 |
| S阴影 |
| S正方形 |
1-
| ||
| 1 |
| 7 |
| 8 |
故答案为：
| 7 |
| 8 |
点评：几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=
求解．
| N(A) |
| N |
练习册系列答案
名校课堂系列答案
相关题目
的最小值，并确定取得最小值时x的值．列表如下，请观察表中y值随x值变化的特点，完成以下的问题．
_______；
在定义域内有最大值或最小值吗？如有，是多少？此时x为何值？(直接回答结果，不需证明)已知函数
．请完成以下任务：
（Ⅰ）探究a=1时，函数f（x）在区间[0，+∞）上的最大值．为此，我们列表如下
| x | 0 | 0.1 | 0.2 | 0.5 | 0.8 | 1 | 1.2 | 1.5 | 1.8 | 2 | 4 | 6 | … |
| y | 0 | 0.396 | 0.769 | 1.6 | 1.951 | 2 | 1.967 | 1.846 | 1.698 | 1.6 | 0.941 | 0.649 | … |
（1）写出函数f（x），在[0，+∞）上的单调区间；指出在各个区间上的单调性，并对其中一个区间的单调性用定义加以证明．
（2）请回答：当x取何值时f（x）取得最大值，f（x）的最大值是多少？
（Ⅱ）按以下两个步骤研究a=1时，函数
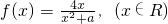的值域．（1）判断函数f（x）的奇偶性；
（2）结合已知和以上研究，画出函数f（x）的大致图象，指出函数的值域．
（Ⅲ）己知a=-1，f（x）的定义域为（-1，1），解不等式
．
已知函数
．请完成以下任务：
（Ⅰ）探究a=1时，函数f（x）在区间[0，+∞）上的最大值．为此，我们列表如下
请观察表中y值随x值变化的特点，解答以下两个问题．
（1）写出函数f（x），在[0，+∞）上的单调区间；指出在各个区间上的单调性，并对其中一个区间的单调性用定义加以证明．
（2）请回答：当x取何值时f（x）取得最大值，f（x）的最大值是多少？
（Ⅱ）按以下两个步骤研究a=1时，函数
的值域．
（1）判断函数f（x）的奇偶性；
（2）结合已知和以上研究，画出函数f（x）的大致图象，指出函数的值域．
（Ⅲ）己知a=-1，f（x）的定义域为（-1，1），解不等式
．
．请完成以下任务：（Ⅰ）探究a=1时，函数f（x）在区间[0，+∞）上的最大值．为此，我们列表如下
| x | 0.1 | 0.2 | 0.5 | 0.8 | 1 | 1.2 | 1.5 | 1.8 | 2 | 4 | 6 | … | |
| y | 0.396 | 0.769 | 1.6 | 1.951 | 2 | 1.967 | 1.846 | 1.698 | 1.6 | 0.941 | 0.649 | … |
（1）写出函数f（x），在[0，+∞）上的单调区间；指出在各个区间上的单调性，并对其中一个区间的单调性用定义加以证明．
（2）请回答：当x取何值时f（x）取得最大值，f（x）的最大值是多少？
（Ⅱ）按以下两个步骤研究a=1时，函数
的值域．（1）判断函数f（x）的奇偶性；
（2）结合已知和以上研究，画出函数f（x）的大致图象，指出函数的值域．
（Ⅲ）己知a=-1，f（x）的定义域为（-1，1），解不等式
．