题目内容
等差数列{an}的前n项和为Sn，a1=1+
，S2=9+
。
（1）求数列{an}的通项an与前n项和为Sn；
（2）设
（n∈N*），求证：数列{bn}中任意不同的三项都不可能成为等比数列。
，S2=9+。（1）求数列{an}的通项an与前n项和为Sn；
（2）设
（n∈N*），求证：数列{bn}中任意不同的三项都不可能成为等比数列。解：（1）由已知得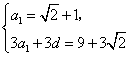
∴
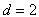
故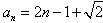
，
。
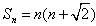（2）由（1）得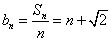
假设数列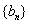
中存在三项
（
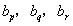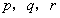互不相等）成等比数列，则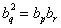
即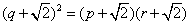
∴
∵
∴
∴
∴
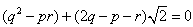
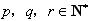
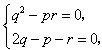
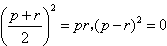
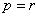
与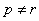
矛盾
所以数列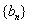
中任意不同的三项都不可能成等比数列。
∴
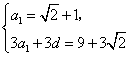
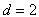
故
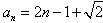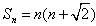，。（2）由（1）得
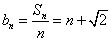
假设数列
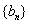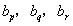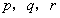中存在三项（互不相等）成等比数列，则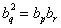即
∴
∵
∴
∴
∴
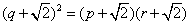
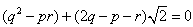
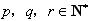
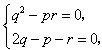
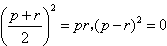
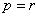
与
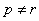矛盾所以数列
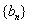中任意不同的三项都不可能成等比数列。
练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn，则a5+a6＞0是S8≥S2的（ ）
| A、充分而不必要条件 | B、必要而不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |