题目内容
设x>-1,函数 的最小值是 .
的最小值是 .
【答案】分析:根据函数的形式,换元:设t=x+1(t>0),将原函数变为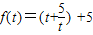 ,再根据t为正数,可以用基本不等式求出f(t)的最小值,最后用等号成立的条件得出相应的x的值,从而得出原函数的最小值
,再根据t为正数,可以用基本不等式求出f(t)的最小值,最后用等号成立的条件得出相应的x的值,从而得出原函数的最小值 是正确的.
是正确的.
解答:解:设t=x+1(t>0),则
 =
=
整理得:
∵t>0
∴
所以
当且仅当 时,函数有最小值
时,函数有最小值
此时x=1
因此函数 当x=1时有最小值为9
当x=1时有最小值为9
故答案为:9
点评:本题以分式函数为载体,考查了函数的最值及其应用,属于中档题.采用换元法、利用基本不等式来求解是解决本题的关键,用这个方法时同学们应该注意等号成立的条件,以免出错.
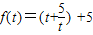 ,再根据t为正数,可以用基本不等式求出f(t)的最小值,最后用等号成立的条件得出相应的x的值,从而得出原函数的最小值
,再根据t为正数,可以用基本不等式求出f(t)的最小值,最后用等号成立的条件得出相应的x的值,从而得出原函数的最小值 是正确的.
是正确的.解答:解:设t=x+1(t>0),则
 =
=
整理得:

∵t>0
∴

所以

当且仅当
 时,函数有最小值
时,函数有最小值此时x=1
因此函数
 当x=1时有最小值为9
当x=1时有最小值为9故答案为:9
点评:本题以分式函数为载体,考查了函数的最值及其应用,属于中档题.采用换元法、利用基本不等式来求解是解决本题的关键,用这个方法时同学们应该注意等号成立的条件,以免出错.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
 的最小值
的最小值 的最小值是________.
的最小值是________. 的最小值是 .
的最小值是 . 的最小值是( )
的最小值是( )