题目内容
△ABC中,角A、B、C所对的边分别为a、b、c,若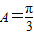 ,a=1,c=2b,则b= .
,a=1,c=2b,则b= .
【答案】分析:通过已知条件,直接利用余弦定理列出方程,然后求出b的值.
解答:解:因为△ABC中,角A、B、C所对的边分别为a、b、c,若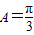 ,a=1,c=2b,
,a=1,c=2b,
所以由余弦定理可得a2=b2+c2-2bccosA,
即1=b2+4b2-2b×2b× =3b2,
=3b2,
所以b=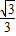 .
.
故答案为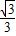 .
.
点评:本题考查余弦定理的应用,正确使用定理是解题的关键.
解答:解:因为△ABC中,角A、B、C所对的边分别为a、b、c,若
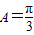 ,a=1,c=2b,
,a=1,c=2b,所以由余弦定理可得a2=b2+c2-2bccosA,
即1=b2+4b2-2b×2b×
 =3b2,
=3b2,所以b=
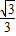 .
.故答案为
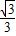 .
.点评:本题考查余弦定理的应用,正确使用定理是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目