题目内容
【题目】已知椭圆C： 
=1（a＞b＞0）的右焦点为F2（1，0），点P（1， 
）在椭圆C上．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过坐标原点O的两条直线EF，MN分别与椭圆C交于E，F，M，N四点，且直线OE，OM的斜率之积为﹣ 
，求证：四边形EMFN的面积为定值．
【答案】解：（Ⅰ）∵为点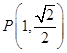 
在椭圆C上，椭圆C的右焦点为F2（1，0）， 则 
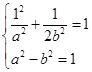，解得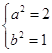 
，
∴椭圆C的方程为 
．
（Ⅱ）当直线EM斜率存在时，设直线方程为l：y=kx+m，E（x1 ， y1），M（x2 ， y2），
联立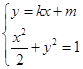 
得（1+2k2）x2+4kmx+2m2﹣2=0， 
，
= 
，
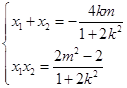由 
得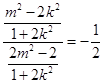 
，即2m2=2k2+1，
原点到直线EM的距离为 
，
∴ 
= 
= 
= 
= 
，
∴ 
．
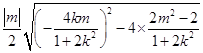
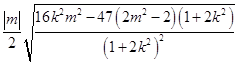
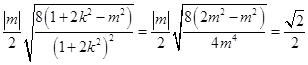当直线EM斜率不存在时， ，x1=x2 ， y1=﹣y2 ， ∴ 
，
又 
，解得 
， 
【解析】（Ⅰ）由题意可得：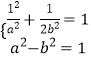 
，解出即可得出．（Ⅱ）当直线EM斜率存在时，设直线方程为l：y=kx+m，E（x1 ， y1），M（x2 ， y2），与椭圆方程联立得（1+2k2）x2+4kmx+2m2﹣2=0，利用斜率计算公式、根与系数的关系及其 
，可得2m2=2k2+1，原点到直线EM的距离为 
，利用 
，代入化简即可得出定值，斜率不存在时也成立．
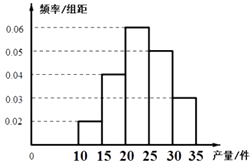
【题目】下列四个命题中错误的是（ ）
A.在一次试卷分析中，从每个考室中抽取第5号考生的成绩进行统计，不是简单随机抽样
B.对一个样本容量为100的数据分组，各组的频数如下：
区间 | [17，19） | [19，21） | [21，23） | [23，25） | [25，27） | [27，29） | [29，31） | [31，33] |
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的58%
C.设产品产量与产品质量之间的线性相关系数为﹣0.91，这说明二者存在着高度相关
D.通过随机询问110名性别不同的行人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如表列联表：
男 | 女 | 总计 | |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 
，则有99%以上的把握认为“选择过马路方式与性别有关”
