题目内容
已知数列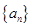 的前
的前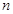 项和
项和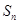 ,且满足
,且满足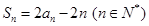 .
.
(1)求数列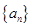 的通项
的通项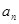 .
.
(2)若数列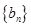 满足
满足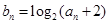 ,
,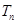 为数列{
为数列{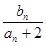 }的前
}的前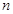 项和,求证
项和,求证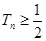 .
.
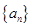 的前
的前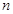 项和
项和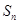 ,且满足
,且满足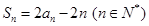 .
.(1)求数列
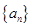 的通项
的通项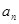 .
.(2)若数列
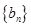 满足
满足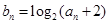 ,
,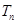 为数列{
为数列{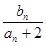 }的前
}的前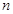 项和,求证
项和,求证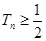 .
.(1)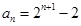 ; (2)证明过程见解析.
; (2)证明过程见解析.
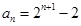 ; (2)证明过程见解析.
; (2)证明过程见解析.试题分析:(1)由所给
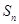 与
与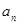 的关系式转化变形,可判断出
的关系式转化变形,可判断出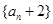 是等比数列,求出此数列的通项公式进一步求出
是等比数列,求出此数列的通项公式进一步求出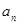 的通项式;(2)将
的通项式;(2)将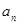 的通项公式代入化可得
的通项公式代入化可得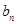 ,则
,则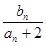 =
=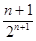 ,观察特点知可由错位相减法求得
,观察特点知可由错位相减法求得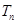 =
=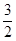 -
-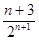 再利用放缩法证明不等式.
再利用放缩法证明不等式.试题解析:
解:(1)
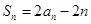 ① ,
① , 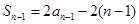 ②
②①-②,得
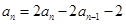 ∴
∴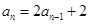
∴
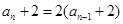 , ∴
, ∴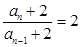
当n=1时,由①得
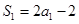 ,则
,则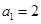 ,
,∴数列
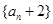 是以
是以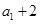 为首项,以2为公比的等比数列.
为首项,以2为公比的等比数列.∴
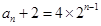 , ∴
, ∴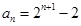 6分
6分(Ⅱ)
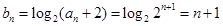 ,
, 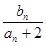 =
=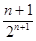 ,
,则
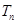 =
=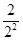 +
+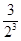 + +
+ +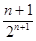 , ③[
, ③[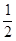
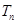 =
=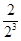 + +
+ +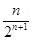 +
+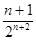 ④
④③-④,得
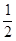
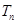 =
=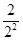 +
+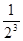 +
+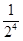 + +
+ +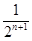 -
-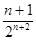 =
=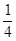 +
+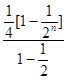 -
-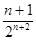
=
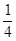 +
+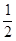 -
-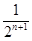 -
-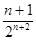 =
=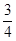 -
-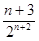 ,
,∴
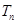 =
=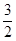 -
-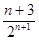 .
.当n≥2时,
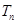 -
-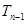 =-
=-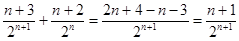 >0,
>0,∴{
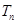 }为递增数列, ∴
}为递增数列, ∴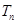 ≥
≥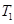 =
=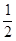 . 14分
. 14分
练习册系列答案
相关题目
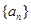 的首项
的首项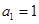 ,公差
,公差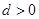 ,且第
,且第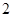 项、第
项、第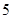 项、第
项、第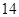 项分别是等比数列
项分别是等比数列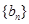 的第
的第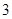 项、第
项、第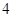 项.
项.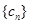 对
对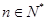 ,均有
,均有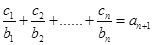 成立,求
成立,求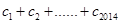 .
.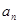 }的前n项和
}的前n项和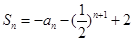 (n为正整数)。
(n为正整数)。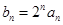 ,求证数列{
,求证数列{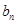 }是等差数列,并求数列{
}是等差数列,并求数列{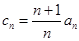 ,
,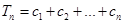 ,求
,求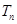 并证明:
并证明: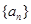 和
和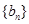 的前n项和分别为
的前n项和分别为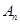 和
和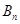 ,且
,且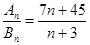 ,则使得
,则使得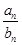 为整数的正整数n的个数是__________。
为整数的正整数n的个数是__________。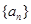 为等差数列,
为等差数列,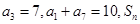 为其前n项和,则使得
为其前n项和,则使得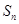 达到最大值的n等于 .
达到最大值的n等于 .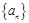 的前
的前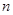 项和为
项和为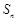 ,首项
,首项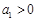 ,
,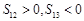 .则以下关于数列
.则以下关于数列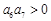 ;②
;②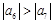 ;③
;③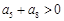 ;④前
;④前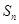 中最大的项为第六项
中最大的项为第六项 满足:
满足: ,则其前10项的和
,则其前10项的和 ( )
( )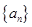 的前
的前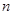 项和为
项和为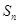 ,且4
,且4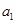 ,2
,2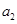 ,
,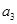 成等差数列。若
成等差数列。若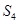 =( )
=( )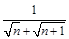 ,若前n项和为10,则项数n为( )
,若前n项和为10,则项数n为( )