题目内容
【题目】如图，在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 ， CA=CC1=2CB，则直线BC1与直线AB1夹角的余弦值为（ ）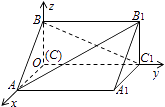
A.
B.
C.
D.
【答案】A
【解析】解：分别以CA、CC1、CB为x轴、y轴和z轴建立如图坐标系，
∵CA=CC1=2CB，∴可设CB=1，CA=CC1=2
∴A（2，0，0），B（0，0，1），B1（0，2，1），C1（0，2，0）
∴ 
=（0，2，﹣1）， 
=（﹣2，2，1）
可得 =0×（﹣2）+2×2+（﹣1）×1=3，且 
= 
， 
=3，
向量 与 所成的角（或其补角）就是直线BC1与直线AB1夹角，
设直线BC1与直线AB1夹角为θ，则cosθ= 
= 
故选A
根据题意可设CB=1，CA=CC1=2，分别以CA、CC1、CB为x轴、y轴和z轴建立如图坐标系，得到A、B、B1、C1四个点的坐标，从而得到向量 与 的坐标，根据异面直线所成的角的定义，结合空间两个向量数量积的坐标公式，可以算出直线BC1与直线AB1夹角的余弦值．
练习册系列答案
相关题目
