题目内容
设数列{an}是公差为d的等差数列,其前n项和为Sn,已知a1=1,d=2(1)求
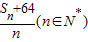 的最小值
的最小值(2)求证:
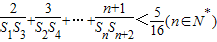 .
.
【答案】分析:(1)由已知和求和公式可得Sn,代入式子由基本不等式可得;(2)可得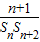 =
=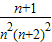 =
=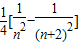 ,代入结合消去规律可得
,代入结合消去规律可得
原式= [
[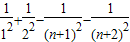 ],由放缩法可得.
],由放缩法可得.
解答:解:(1)由题意可得Sn=na1+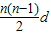 =n2,
=n2,
故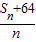 =
=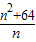 =n+
=n+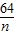 ≥2
≥2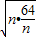 =16,
=16,
当且仅当n=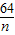 ,即n=8时取等号,
,即n=8时取等号,
故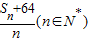 的最小值为16
的最小值为16
(2)由(1)可知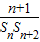 =
=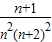 =
=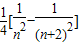 ,
,
故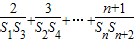
=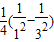 +
+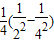 +…+
+…+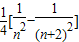
= [
[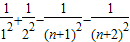 ]<
]< (
(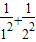 )=
)=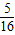
点评:本题考查等差数列的前n项和公式,涉及基本不等式和放缩法证明不等式,属中档题.
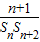 =
=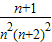 =
=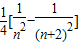 ,代入结合消去规律可得
,代入结合消去规律可得原式=
 [
[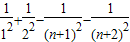 ],由放缩法可得.
],由放缩法可得.解答:解:(1)由题意可得Sn=na1+
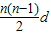 =n2,
=n2,故
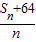 =
=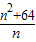 =n+
=n+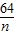 ≥2
≥2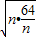 =16,
=16,当且仅当n=
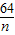 ,即n=8时取等号,
,即n=8时取等号,故
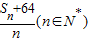 的最小值为16
的最小值为16(2)由(1)可知
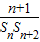 =
=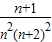 =
=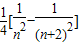 ,
,故
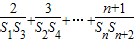
=
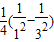 +
+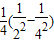 +…+
+…+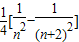
=
 [
[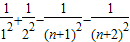 ]<
]< (
(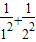 )=
)=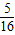
点评:本题考查等差数列的前n项和公式,涉及基本不等式和放缩法证明不等式,属中档题.

练习册系列答案
相关题目