题目内容
已知双曲线
-
=1的右焦点为F,点A(9,2),试在这个双曲线上求一点M,使?|MA|+
|MF|的值最小,并求出这个最小值.
思路分析:|MF|是双曲线的焦半径,据此进行思考,可用双曲线第二定义进行转化.
解:如图所示,l为双曲线的右准线,M为双曲线上任意一点,分别作MN⊥l,AB⊥l于N、B两点.
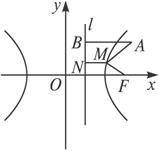
∵e=,∴由双曲线的第二定义有=e,
即|MN|=
|MF|.
∴|MA|+
|MF|
=|MA|+|MN|≥|AB|.
当且仅当M为AB与双曲线右支的交点时,|MA|+
|MF|取得最小值.此时,点M的坐标为(
,2),最小值为9-
=9-
.
练习册系列答案
相关题目
=1的右焦点是F，右顶点是A,虚轴的上端点是B，
·
=6-4
，∠BAF=150°.
+2
=0，求直线l的斜率.
-
=1的右焦点为
,则该双曲线的离心率等于（ ）
B．
C．
D．
-
=1的右焦点为F，若过点F的直线与双曲线的右支有且只有一个交点，则此直线斜率的取值范围是
，
） （B）（-
，
） （C）[-
， 
] （D）[-
，
]