题目内容
设f(x)是定义在(0,+∞)上的增函数,且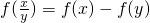 ,若f(2)=1,则f(4)=________.
,若f(2)=1,则f(4)=________.
解:由于f(x)是定义在(0,+∞)上的增函数,且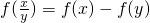 ,若f(2)=1,所以令x=4,y=2,得:
,若f(2)=1,所以令x=4,y=2,得: ?f(2)=f(4)-f(2)?f(4)=2f(2)=2.
?f(2)=f(4)-f(2)?f(4)=2f(2)=2.
故答案为:2.
分析:因为f(x)是定义在(0,+∞)上的增函数,利用增函数的定义可以知道自变量与函数值之间应为一一对应的关系,又由于且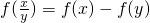 ,若f(2)=1,所以利用已知条件对于该式子利用恰当的赋值即可求解.
,若f(2)=1,所以利用已知条件对于该式子利用恰当的赋值即可求解.
点评:此题考查了增函数的定义,还考查了已知任意两变量的抽象函数式,利用恰当的赋值法进行求值.
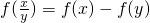 ,若f(2)=1,所以令x=4,y=2,得:
,若f(2)=1,所以令x=4,y=2,得: ?f(2)=f(4)-f(2)?f(4)=2f(2)=2.
?f(2)=f(4)-f(2)?f(4)=2f(2)=2.故答案为:2.
分析:因为f(x)是定义在(0,+∞)上的增函数,利用增函数的定义可以知道自变量与函数值之间应为一一对应的关系,又由于且
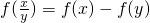 ,若f(2)=1,所以利用已知条件对于该式子利用恰当的赋值即可求解.
,若f(2)=1,所以利用已知条件对于该式子利用恰当的赋值即可求解.点评:此题考查了增函数的定义,还考查了已知任意两变量的抽象函数式,利用恰当的赋值法进行求值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 设f(x)是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图象,则f(2013)+f(2014)=( )
设f(x)是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图象,则f(2013)+f(2014)=( )