题目内容
已知函数f(x)=-x3+ax2-4(a∈R),f(x)是f′(x)的导函数。
(1)当a=2时,对于任意的m∈[-1,1],求f(m)的范围;
(2)若存在x0∈(0,+∞),使f(x0)>0,求a的取值范围。
(1)当a=2时,对于任意的m∈[-1,1],求f(m)的范围;
(2)若存在x0∈(0,+∞),使f(x0)>0,求a的取值范围。
解:(1)由题意知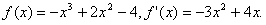
令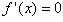 得
得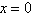 或
或
当x在[-1,1]上变化时,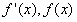 随x的变化情况如下表:
随x的变化情况如下表:
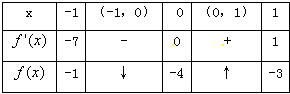
∴对于m∈[-1,1],f(m)的范围为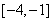 。
。
(2)∵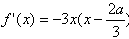
①若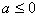 ,当x>0时,
,当x>0时,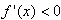
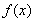 在
在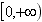 上单调递减
上单调递减
又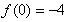
则当x>0时,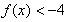
∴当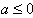 时,不存在
时,不存在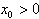 ,使
,使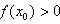
②若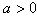 ,则当
,则当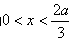 时,
时,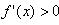
当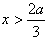 时,
时,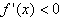
从而f(x)在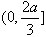 上单调递增
上单调递增
在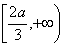 上单调递减
上单调递减
当x∈(0,+∞)时,f(x)max=f(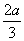 )=
)=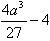
根据题意,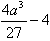 >0,即
>0,即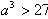 ,解得a>3
,解得a>3
综上,a的取值范围是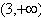 。
。
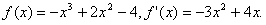
令
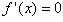 得
得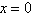 或
或
当x在[-1,1]上变化时,
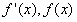 随x的变化情况如下表:
随x的变化情况如下表: 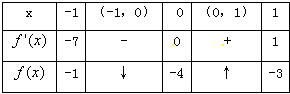
∴对于m∈[-1,1],f(m)的范围为
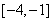 。
。(2)∵
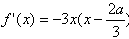
①若
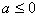 ,当x>0时,
,当x>0时,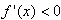
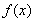 在
在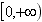 上单调递减
上单调递减又
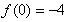
则当x>0时,
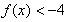
∴当
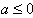 时,不存在
时,不存在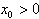 ,使
,使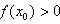
②若
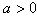 ,则当
,则当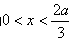 时,
时,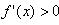
当
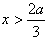 时,
时,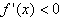
从而f(x)在
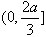 上单调递增
上单调递增在
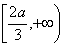 上单调递减
上单调递减当x∈(0,+∞)时,f(x)max=f(
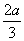 )=
)=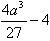
根据题意,
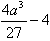 >0,即
>0,即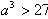 ,解得a>3
,解得a>3综上,a的取值范围是
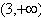 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|