题目内容
一艘海轮从A处出发,以每小时40海里的速度沿东偏南50°方向直线航行,30分钟后到达B处.在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是( )
A、10
| ||
B、10
| ||
C、20
| ||
D、20
|
分析:先根据题意画出图象确定∠BAC、∠ABC的值,进而可得到∠ACB的值,最后根据正弦定理可得到BC的值.
解答: 解:如图,由已知可得,∠BAC=30°,∠ABC=105°,
解:如图,由已知可得,∠BAC=30°,∠ABC=105°,
AB=20,从而∠ACB=45°.
在△ABC中,由正弦定理,
得BC=
×sin30°=10
.
故选A.
 解:如图,由已知可得,∠BAC=30°,∠ABC=105°,
解:如图,由已知可得,∠BAC=30°,∠ABC=105°,AB=20,从而∠ACB=45°.
在△ABC中,由正弦定理,
得BC=
| AB |
| sin45° |
| 2 |
故选A.
点评:本题主要考查正弦定理的应用.考查对基础知识的掌握程度.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
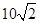 海里 B.
海里 B.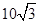 海里 C.
海里 C.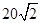 海里 D.
海里 D.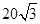 海里
海里 海里 B.
海里 B.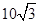 海里 C.
海里 C.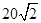 海里 D.
海里 D. 海里
海里