题目内容
已知f(x)是定义在[-1,1]上的奇函数且f(1)=1,对x1、x2∈[-1,1],且x1+x2≠0时,有 ,若f(x)≤m2-2am+1对所有x∈[-1,1]、a∈[-1,1]恒成立,则实数m的取值范围是________.
,若f(x)≤m2-2am+1对所有x∈[-1,1]、a∈[-1,1]恒成立,则实数m的取值范围是________.
{m}m≤-2或m≥2或m=0}
分析:利用函数单调性的定义证明函数f(x)是[-1,1]上的增函数,根据函数f(x)≤m2+2am+1对所有的x∈[-1,1],a∈[-1,1]恒成立,说明f(x)的最大值1小于或等于右边,因此先将右边看作a的函数,m为参数系数,解不等式组,即可得出m的取值范围.
解答:任取x1、x2∈[-1,1],且x1<x2,则f(x1)-f(x2)=f(x1)+f(-x2)
∵ ,
,
即 ,∴
,∴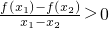
∵x1-x2<0,
∴f(x1)-f(x2)<0.
∴f(x)是[-1,1]上的增函数,
要使f(x)≤m2+2am+1对所有的x∈[-1,1],a∈[-1,1]恒成立,
只须f(x)max≤m2+2am+1,即1≤m2+2am+1对任意的a∈[-1,1]恒成立,
亦即m2+2am≥0对任意的a∈[-1,1]恒成立.令g(a)=2ma+m2,
只须 ,解得m≤-2或m≥2或m=0,
,解得m≤-2或m≥2或m=0,
故答案为m≤-2或m≥2或m=0.
点评:本题考查了抽象函数的单调性与函数的值域、不等式恒成立等知识点,属于中档题,解题时应该注意题中的主元与次元的处理.
分析:利用函数单调性的定义证明函数f(x)是[-1,1]上的增函数,根据函数f(x)≤m2+2am+1对所有的x∈[-1,1],a∈[-1,1]恒成立,说明f(x)的最大值1小于或等于右边,因此先将右边看作a的函数,m为参数系数,解不等式组,即可得出m的取值范围.
解答:任取x1、x2∈[-1,1],且x1<x2,则f(x1)-f(x2)=f(x1)+f(-x2)
∵
 ,
,即
 ,∴
,∴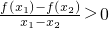
∵x1-x2<0,
∴f(x1)-f(x2)<0.
∴f(x)是[-1,1]上的增函数,
要使f(x)≤m2+2am+1对所有的x∈[-1,1],a∈[-1,1]恒成立,
只须f(x)max≤m2+2am+1,即1≤m2+2am+1对任意的a∈[-1,1]恒成立,
亦即m2+2am≥0对任意的a∈[-1,1]恒成立.令g(a)=2ma+m2,
只须
 ,解得m≤-2或m≥2或m=0,
,解得m≤-2或m≥2或m=0,故答案为m≤-2或m≥2或m=0.
点评:本题考查了抽象函数的单调性与函数的值域、不等式恒成立等知识点,属于中档题,解题时应该注意题中的主元与次元的处理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目