题目内容
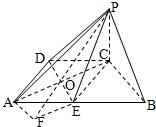 如图在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=
如图在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=| π |
| 2 |
| 1 |
| 2 |
(1)求证:平面PAC⊥平面PDE;
(2)求二面角A-PE-D的大小.
分析:(1)在面PDE内找一条线DE,通过证明DE⊥AC,DE⊥PC,从而证明DE和面PAC垂直,即可证得面PDE⊥面PAC.
(2)用三垂线定理作二面角的平面角∠AEF,在△PAO中有面积相等不难算出AF=
a,而AE=a,解Rt△AFE可得∠AEF的大小.
(2)用三垂线定理作二面角的平面角∠AEF,在△PAO中有面积相等不难算出AF=
| ||
| 3 |
解答: (1)证明:在直角梯形ABCD中,容易知道四边形AECD是正方形,
(1)证明:在直角梯形ABCD中,容易知道四边形AECD是正方形,
∴DE⊥AC,
又PC⊥面ABCD,
∴DE⊥PC∴DE⊥面PAC,
∴面PDE⊥面PAC;
(2)解:记PC=a,用三垂线定理作二面角的平面角.
记AC、DE交于O,连PO,PO是相互垂直的平面PDE和PAC的交线,
过A作PO的垂线交PO(的延长线)于F,
则AF⊥面PDE,即F是A在面PDE内的射影,
又容易证明AE⊥面PEC,则AE⊥PE,于是FE⊥PE,
∴∠AEF是二面角A-PE-D的平面角;
在△PAO中有面积相等不难算出AF=
a,
而AE=a,在Rt△AFE中,∠AEF=arcsin
.
 (1)证明:在直角梯形ABCD中,容易知道四边形AECD是正方形,
(1)证明:在直角梯形ABCD中,容易知道四边形AECD是正方形,∴DE⊥AC,
又PC⊥面ABCD,
∴DE⊥PC∴DE⊥面PAC,
∴面PDE⊥面PAC;
(2)解:记PC=a,用三垂线定理作二面角的平面角.
记AC、DE交于O,连PO,PO是相互垂直的平面PDE和PAC的交线,
过A作PO的垂线交PO(的延长线)于F,
则AF⊥面PDE,即F是A在面PDE内的射影,
又容易证明AE⊥面PEC,则AE⊥PE,于是FE⊥PE,
∴∠AEF是二面角A-PE-D的平面角;
在△PAO中有面积相等不难算出AF=
| ||
| 3 |
而AE=a,在Rt△AFE中,∠AEF=arcsin
| ||
| 3 |
点评:用三垂线定理作二面角的平面角,是作二面角的平面角的最常用、最重要的方法.其过程概括为:找一垂找(作)一个面内一点P在另一个面内的射影P/,作二垂过P(或P/)作二面角棱l的垂线,垂足为Q,连三垂连P/Q,则l⊥P/Q,于是∠PQP/为二面角的平面角;计算该角在直角三角形内进行;在上述过程中,“找一垂”是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
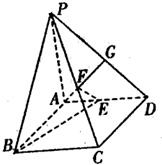 如图在四棱锥P-ABCD中,底ABCD是矩形,PA⊥面ABCD,AP=AB=2,BC=2
如图在四棱锥P-ABCD中,底ABCD是矩形,PA⊥面ABCD,AP=AB=2,BC=2 如图在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点;PA=kAB(k>0),且二面角E-BD-C的平面角大于30°,则k的取值范围是( )
如图在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点;PA=kAB(k>0),且二面角E-BD-C的平面角大于30°,则k的取值范围是( ) 如图在四棱锥P-ABCD中侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD为直角梯形.其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点
如图在四棱锥P-ABCD中侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD为直角梯形.其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点 如图在四棱锥P-ABCD中,侧棱PD⊥平面ABCD,M,N分别是AB,PC的中点,底面ABCD是菱形,
如图在四棱锥P-ABCD中,侧棱PD⊥平面ABCD,M,N分别是AB,PC的中点,底面ABCD是菱形, 如图在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,垂足为点A,PA=AB=1,点M,N分别是PD,PB的中点.
如图在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,垂足为点A,PA=AB=1,点M,N分别是PD,PB的中点.