题目内容
若数列{an},{bn}的通项公式分别是an=(-1)n+2012a,bn=2+
,且an<bn对任意n∈N*恒成立,则实数a的取值范围是( )
| (-1)n+2013 |
| n |
分析:当n为奇数时,an=-a<2+
恒成立,可得-a≤2.当n为偶数时,an=a<2-
恒成立,可得a<2-
=
.求其交集即可.
| 1 |
| n |
| 1 |
| n |
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:①当n为奇数时,an=-a<2+
恒成立,∴-a≤2,解得a≥-2.
②当n为偶数时,an=a<2-
恒成立,∴a<2-
=
.
∵an<bn对任意n∈N*恒成立,∴
,解得-2≤a<
.
故选:C.
| 1 |
| n |
②当n为偶数时,an=a<2-
| 1 |
| n |
| 1 |
| 2 |
| 3 |
| 2 |
∵an<bn对任意n∈N*恒成立,∴
|
| 3 |
| 2 |
故选:C.
点评:本题考查了数列恒成立问题、分类讨论、数列的单调性、交集的意义等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
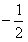 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;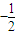 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;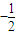 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;