题目内容

数列{a_n}中，a₁=1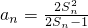， $数学公式$ （n≥2），则这个数列的前n项和为________．

$\text{[math]}$
分析：利用a_n=S_n-S_n-1（n≥2）代入已知条件，整理出 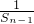$\text{[math]}$ - $\text{[math]}$ 等于常数，构造新数列，通过新数列的特征，求出新数列的通项公式，转化后，求出这个数列的前n项和．
解答：将a_n=S_n-S_n-1代入已知条件 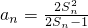$\text{[math]}$ 得
S_n-S_n-1= $\text{[math]}$ （n≥2），展开化简得
2S_n²-2S_n•S_n-1-S_n+S_n-1=2S_n²，
S_n-1-Sn=2S_n-1•Sn，
两边同除以S_n•S_n-1得
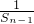$\text{[math]}$ - $\text{[math]}$ =2 （n≥2），
所以{ $\text{[math]}$ }是公差为2的等差数列，其首项= $\text{[math]}$ = $\text{[math]}$ =1，
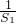所以 $\text{[math]}$ =1+2（n-1）=2n-1，
S_n= $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：本题是中档题，考查数列的前n项和的求法，构造新数列的解题的难点也是关键点，考查转化思想，计算能力．