Question

（本小题满分12分）

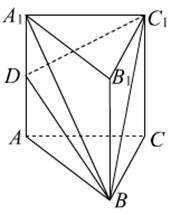在正三棱柱ABC—A₁B₁C₁中，D是棱AA₁上一点，平面BC₁D⊥平面BB₁C₁C，AB=AA₁=2.

（Ⅰ）求点A到平面BC₁D的距离；

（Ⅱ）求直线A₁B与平面BC₁D所成的角的正弦值.

Answer 1

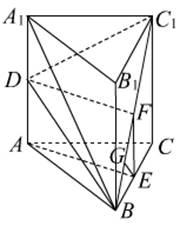
解1：（Ⅰ）作DF⊥BC₁于F，

∵平面BC₁D⊥平面BB₁C₁C，

∴DF⊥平面BB₁C₁C，……………………2分

取BC中点E，连接AE，EF，

则AE⊥平面BB₁C₁C，

∴AE∥DF，AE∥平面BC₁D，

于是A、E到平面BC₁D的距离相等，…4分

作EG⊥BC₁于G，则EG⊥平面BC₁D，

又EG=B₁C=，

因此，A到平面BC₁D的距离为；……………………6分

(Ⅱ) ∵AA₁∥平面BB₁C₁C，

∴AD∥EF，得EF∥CC₁，F是BC₁的中点.………………8分

于是AD=EF=CC₁=1，D是AA₁中点，

所以A₁和A到平面BC₁D的距离相等.

设A₁到平面BC₁D的距离为d，则d=，…………………10分

               设A₁B与平面BC₁D所成的角为θ，则sinθ=.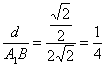

                                                       ……………………12分

       解2：（Ⅰ）以AC中点O为原点，建立空间直角坐

标系如图.                                   ……………………1分

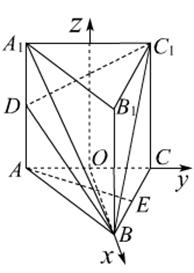设AD=h,则A（0,-1,0），B（，0,0），

C（0,1,0），A₁（0，-1,2），C1（0,1,2），

D（0，-1，h）.  ……………………2分

,

设平面BC₁D的法向量为n=（x，y，z），

则，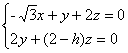

令z=2，则y=h-2，x=.

n=（，h-2，2）……………………3分

取BC中点E（），

）是平面BB₁C₁C的一个法向量.

∵平面BC₁D⊥平面BB₁C₁C，

∴×+(h-2)×=0，得h=1.………………5分

n=（，-1，2），=(0,0,1).

A到平面BC₁D的距离为d=.…………6分

(Ⅱ) ,

设A₁B与平面BC₁D所成的角为θ，则

sinθ=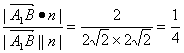.         …………………12分