题目内容
设函数f(x)=2sin(ωx+ )(ω>0,x∈R),且以π为最小正周期.
)(ω>0,x∈R),且以π为最小正周期.
(Ⅰ)求f( )的值;
)的值;
(Ⅱ)已知f( +
+ )=
)=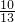 ,a∈(-
,a∈(- ,0),求sin(a-
,0),求sin(a- )的值.
)的值.
解(Ⅰ)∵T= =π,∴ω=2,(2分)
=π,∴ω=2,(2分)
∴函数f(x)=2sin(2x+ ). (3分)
). (3分)
∴f( )=2sin(2×
)=2sin(2× +
+ )=-2sin
)=-2sin =-
=- . (5分)
. (5分)
(Ⅱ)∵f( +
+ )=
)=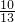 =2sin(a+
=2sin(a+ )=2cosa,∴cosa=
)=2cosa,∴cosa= .(7分)
.(7分)
∵a∈(- ,0),∴sina=-
,0),∴sina=- =-
=- . (9分)
. (9分)
∴sin(a- )=sina•cos
)=sina•cos -cosa•sin
-cosa•sin  =
=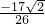 . (12分)
. (12分)
分析:(Ⅰ)由函数的周期 T= =π,求出ω=2,得到函数f(x)=2sin(2x+
=π,求出ω=2,得到函数f(x)=2sin(2x+ ),从而求得f(
),从而求得f( )的值.
)的值.
(Ⅱ)由f( +
+ )=
)=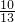 求出cosa,利用同角三角函数的基本关系求出 sina,再由两角差的正弦公式求出 sin(a-
求出cosa,利用同角三角函数的基本关系求出 sina,再由两角差的正弦公式求出 sin(a- )的值.
)的值.
点评:本题主要考查利用y=Asin(ωx+φ)的图象性质求函数的解析式,三角函数的恒等变换及化简求值,两角差的正弦公式的应用,属于中档题.
 =π,∴ω=2,(2分)
=π,∴ω=2,(2分)∴函数f(x)=2sin(2x+
 ). (3分)
). (3分)∴f(
 )=2sin(2×
)=2sin(2× +
+ )=-2sin
)=-2sin =-
=- . (5分)
. (5分)(Ⅱ)∵f(
 +
+ )=
)=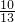 =2sin(a+
=2sin(a+ )=2cosa,∴cosa=
)=2cosa,∴cosa= .(7分)
.(7分)∵a∈(-
 ,0),∴sina=-
,0),∴sina=- =-
=- . (9分)
. (9分)∴sin(a-
 )=sina•cos
)=sina•cos -cosa•sin
-cosa•sin  =
=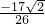 . (12分)
. (12分)分析:(Ⅰ)由函数的周期 T=
 =π,求出ω=2,得到函数f(x)=2sin(2x+
=π,求出ω=2,得到函数f(x)=2sin(2x+ ),从而求得f(
),从而求得f( )的值.
)的值.(Ⅱ)由f(
 +
+ )=
)=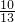 求出cosa,利用同角三角函数的基本关系求出 sina,再由两角差的正弦公式求出 sin(a-
求出cosa,利用同角三角函数的基本关系求出 sina,再由两角差的正弦公式求出 sin(a- )的值.
)的值.点评:本题主要考查利用y=Asin(ωx+φ)的图象性质求函数的解析式,三角函数的恒等变换及化简求值,两角差的正弦公式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目