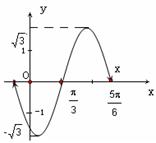
题目内容
设 其中
其中
(Ⅰ)求函数 的值域;
的值域;
(Ⅱ)若 在
在 上为增函数,求
上为增函数,求 的最大值
的最大值
 其中
其中
(Ⅰ)求函数
 的值域;
的值域;(Ⅱ)若
 在
在 上为增函数,求
上为增函数,求 的最大值
的最大值(Ⅰ)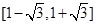 (Ⅱ)
(Ⅱ)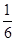
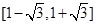 (Ⅱ)
(Ⅱ)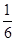
(Ⅰ)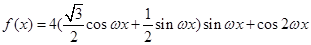

因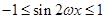 ,所以函数
,所以函数 的值域为
的值域为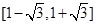
(Ⅱ)因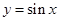 在每个闭区间
在每个闭区间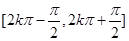 (
(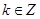 )上为增函数,故
)上为增函数,故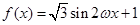 (
( ) 在每个闭区间
) 在每个闭区间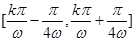 (
(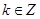 )上为增函数
)上为增函数
依题意知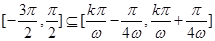 对某个
对某个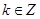 成立,此时必有
成立,此时必有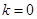
于是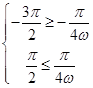 解得
解得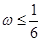 ,故
,故 的最大值为
的最大值为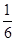
【考点定位】本题以三角函数的化简求值为主线,三角函数的性质为考查目的一道综合题,考查学生分析问题解决问题的能力.由正弦函数的单调性结合条件可列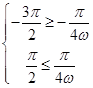 ,从而解得ω的取值范围,即可得ω的最大值.
,从而解得ω的取值范围,即可得ω的最大值.
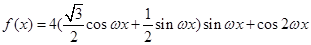

因
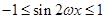 ,所以函数
,所以函数 的值域为
的值域为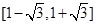
(Ⅱ)因
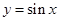 在每个闭区间
在每个闭区间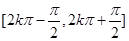 (
(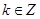 )上为增函数,故
)上为增函数,故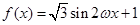 (
( ) 在每个闭区间
) 在每个闭区间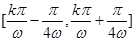 (
(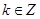 )上为增函数
)上为增函数依题意知
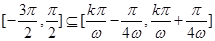 对某个
对某个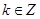 成立,此时必有
成立,此时必有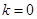
于是
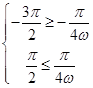 解得
解得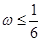 ,故
,故 的最大值为
的最大值为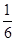
【考点定位】本题以三角函数的化简求值为主线,三角函数的性质为考查目的一道综合题,考查学生分析问题解决问题的能力.由正弦函数的单调性结合条件可列
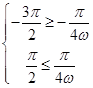 ,从而解得ω的取值范围,即可得ω的最大值.
,从而解得ω的取值范围,即可得ω的最大值.
练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 sinωx+cosωx)cosωx-0.5(ω>0)的最小正周期为4π,(1)求f(x)的单调递增区间;(2)在∆ABC中,角A,B,C的对边分别是a,b,c,满足(2a-c)cosB=bcosC,求角B的值,并求函数f(A)的取值范围
sinωx+cosωx)cosωx-0.5(ω>0)的最小正周期为4π,(1)求f(x)的单调递增区间;(2)在∆ABC中,角A,B,C的对边分别是a,b,c,满足(2a-c)cosB=bcosC,求角B的值,并求函数f(A)的取值范围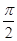 ,j=
,j=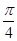
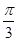 ,j=
,j=
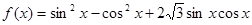 。求函数
。求函数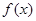 的单调递增区间和最小值;
的单调递增区间和最小值;
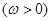 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为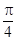 .
.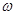 值;(2)若
值;(2)若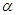 是第四象限角,
是第四象限角,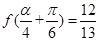 ,求
,求 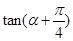 的值
的值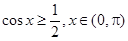 ,且
,且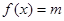 有且仅有一个实根,求实数
有且仅有一个实根,求实数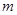 的值.
的值. ( )
( )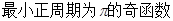



 的最大值是( )
的最大值是( )



 ,则
,则 ( )
( )

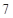 或
或
 或
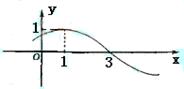
或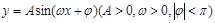 的部分图象, 则
的部分图象, 则