题目内容
已知:函数f(x)=2cos2x+asinxcosx,f =0.
=0.
(Ι)求实数a;
(ΙΙ)求函数f(x)的最小正周期及单调增区间;
(III)若函数f(x)的图象按向量m=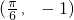 平移后,得到一个函数g(x)的图象,求g(x)的解析式.
平移后,得到一个函数g(x)的图象,求g(x)的解析式.
解:(Ι)由题意,f =2×
=2× +a×
+a× ×
× =0,∴a=-2
=0,∴a=-2 .
.
(ΙΙ)函数f(x)=2cos2x+asinxcosx=(cos2x+1)- sin2x=2cos(2x+
sin2x=2cos(2x+ )+1,
)+1,
故最小正周期T= .
.
令 2kπ-π≤2x+ ≤2kπ,k∈z,解得 kπ-
≤2kπ,k∈z,解得 kπ- ≤x≤kπ-
≤x≤kπ- ,k∈z.
,k∈z.
故函数的增区间为[kπ- ,kπ-
,kπ- ],k∈z.
],k∈z.
(ΙII)在函数g(x)的图象上任取一点P(x,y),设该点是由函数f(x)图象上的点
P′(x′,y′)按向量 =(
=( ,-1)平移后所得,则
,-1)平移后所得,则  ,∴
,∴ .
.
代入 y′=2cos(2x′+ )+1中可得:y=2cos2x,
)+1中可得:y=2cos2x,
∴g(x)=2cos2x.
分析:(Ι)直接利用条件 f =2×
=2× +a×
+a× ×
× =0,解方程求出a的值.
=0,解方程求出a的值.
(ΙΙ)根据三角函数的恒等变换化简函数f(x)的解析式为2cos(2x+ )+1,令 2kπ-π≤2x+
)+1,令 2kπ-π≤2x+ ≤2kπ,k∈z,求出x的范围,即可得到函数的增区间.
≤2kπ,k∈z,求出x的范围,即可得到函数的增区间.
(ΙII)在函数g(x)的图象上任取一点P(x,y),设该点是由函数f(x)图象上的点P′(x′,y′)按向量 =(
=( ,-1)平移后所得,得到这两个点的坐标间的关系,代入y′=2cos(2x′+
,-1)平移后所得,得到这两个点的坐标间的关系,代入y′=2cos(2x′+ )+1中可得 g(x) 解析式.
)+1中可得 g(x) 解析式.
点评:本题主要考查三角函数的恒等变换,函数y=Asin(ωx+∅)的图象变换规律,以及函数y=Asin(ωx+∅)的性质应用,属于中档题.
 =2×
=2× +a×
+a× ×
× =0,∴a=-2
=0,∴a=-2 .
.(ΙΙ)函数f(x)=2cos2x+asinxcosx=(cos2x+1)-
 sin2x=2cos(2x+
sin2x=2cos(2x+ )+1,
)+1,故最小正周期T=
 .
.令 2kπ-π≤2x+
 ≤2kπ,k∈z,解得 kπ-
≤2kπ,k∈z,解得 kπ- ≤x≤kπ-
≤x≤kπ- ,k∈z.
,k∈z.故函数的增区间为[kπ-
 ,kπ-
,kπ- ],k∈z.
],k∈z.(ΙII)在函数g(x)的图象上任取一点P(x,y),设该点是由函数f(x)图象上的点
P′(x′,y′)按向量
 =(
=( ,-1)平移后所得,则
,-1)平移后所得,则  ,∴
,∴ .
.代入 y′=2cos(2x′+
 )+1中可得:y=2cos2x,
)+1中可得:y=2cos2x,∴g(x)=2cos2x.
分析:(Ι)直接利用条件 f
 =2×
=2× +a×
+a× ×
× =0,解方程求出a的值.
=0,解方程求出a的值.(ΙΙ)根据三角函数的恒等变换化简函数f(x)的解析式为2cos(2x+
 )+1,令 2kπ-π≤2x+
)+1,令 2kπ-π≤2x+ ≤2kπ,k∈z,求出x的范围,即可得到函数的增区间.
≤2kπ,k∈z,求出x的范围,即可得到函数的增区间.(ΙII)在函数g(x)的图象上任取一点P(x,y),设该点是由函数f(x)图象上的点P′(x′,y′)按向量
 =(
=( ,-1)平移后所得,得到这两个点的坐标间的关系,代入y′=2cos(2x′+
,-1)平移后所得,得到这两个点的坐标间的关系,代入y′=2cos(2x′+ )+1中可得 g(x) 解析式.
)+1中可得 g(x) 解析式.点评:本题主要考查三角函数的恒等变换,函数y=Asin(ωx+∅)的图象变换规律,以及函数y=Asin(ωx+∅)的性质应用,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目