题目内容
在数列{an}中, ,
, ,令
,令 ,且数列{bn}的前n项和记作Tn,则Tn的取值范围是________.
,且数列{bn}的前n项和记作Tn,则Tn的取值范围是________.
[ )
)
分析:由 可判断数列{
可判断数列{ }为等差数列,从而可求得
}为等差数列,从而可求得 ,进而得到an,bn,利用裂项相消法可求得Tn,根据数列的单调性即可求得Tn的取值范围.
,进而得到an,bn,利用裂项相消法可求得Tn,根据数列的单调性即可求得Tn的取值范围.
解答:由 ,知数列{
,知数列{ }为等差数列,首项为1,公差为
}为等差数列,首项为1,公差为 =2-1=1,
=2-1=1,
所以 =1+(n-1)•1=n,则an=
=1+(n-1)•1=n,则an= ,
,
所以 =
=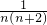 =
= (
( ),
),
所以Tn=b1+b2+b3+…+bn= (1-
(1- )+
)+ (
(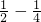 )+
)+ (
(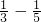 )+…+
)+…+ (
( )
)
= (1-
(1- +
+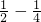 +
+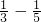 +
+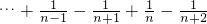 )
)
= (1
(1 -
- -
- )
)
= ,
,
因为-(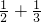 )≤-
)≤-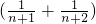 <0,
<0,
所以 -
- ≤
≤
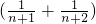 <
< ,即
,即 ≤
≤
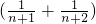 <
< ,
,
故 Tn<
Tn< .
.
故答案为:[ ,
, ).
).
点评:本题考查利用数列递推公式求数列通项、等差数列的通项公式及裂项相消法求和等知识,考查学生逻辑推理能力,属中档题.
 )
)分析:由
 可判断数列{
可判断数列{ }为等差数列,从而可求得
}为等差数列,从而可求得 ,进而得到an,bn,利用裂项相消法可求得Tn,根据数列的单调性即可求得Tn的取值范围.
,进而得到an,bn,利用裂项相消法可求得Tn,根据数列的单调性即可求得Tn的取值范围.解答:由
 ,知数列{
,知数列{ }为等差数列,首项为1,公差为
}为等差数列,首项为1,公差为 =2-1=1,
=2-1=1,所以
 =1+(n-1)•1=n,则an=
=1+(n-1)•1=n,则an= ,
,所以
 =
=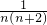 =
= (
( ),
),所以Tn=b1+b2+b3+…+bn=
 (1-
(1- )+
)+ (
(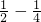 )+
)+ (
(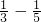 )+…+
)+…+ (
( )
)=
 (1-
(1- +
+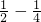 +
+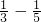 +
+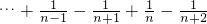 )
)=
 (1
(1 -
- -
- )
)=
 ,
,因为-(
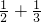 )≤-
)≤-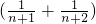 <0,
<0,所以
 -
- ≤
≤
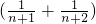 <
< ,即
,即 ≤
≤
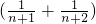 <
< ,
,故
 Tn<
Tn< .
.故答案为:[
 ,
, ).
).点评:本题考查利用数列递推公式求数列通项、等差数列的通项公式及裂项相消法求和等知识,考查学生逻辑推理能力,属中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目